题目内容
6.如图1所示是小徐同学做“探究做功与速度变化的关系”的实验装置.他将光电门固定在直轨道上的O点,用同一重物通过细线拉同一小车,每次小车都从不同位置由静止释放,各位置A、B、C、D、E、F、G(图中只标出了O、G)离O点的距离d分别为8cm、16cm、24cm、32cm、40cm、48cm,56cm.
(1)该实验是否需要测量重物的重力.不需要(填“需要”或“不需要”);
(2)该实验是否必须平衡摩擦力?否(填“是”或“否”);
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| d/×10-2m | 8.00 | 16.00 | 24.00 | 32.00 | 40.00 | 48.00 | 56.00 |
| v/(m/s) | 0.49 | 0.69 | 0.85 | 0.99 | 1.09 | 1.21 | 1.50 |
| v2/(m/s)2 | 0.24 | 0.48 | 0.72 | 0.98 | 1.19 | 1.46 | 2.25 |
| $\sqrt{v}$(m/s)${\;}^{\frac{1}{2}}$ | 0.70 | 0.83 | 0.92 | 1.00 | 1.04 | 1.10 | 1.23 |
(4)从图象得到的直接结论是d与v2成正比,从而间接得到做功与物体速度变化的规律是做功和速度的二次方成正比.
分析 该“探究做功与速度变化的关系”的实验中,要验证物块在外力的作用下经过连续相等的位移时,外力做功与物体的速度变化的关系,即:W=Fs与物体的速度v之间的关系.
而$s=\frac{{v}_{t}^{2}-{v}_{0}^{2}}{2a}$,与物体的重力无关,与是否存在摩擦力也无关.根据记录的数据判定d与v的关系.
解答 解:(1)该实验中,根据W=Fs,F=ma和$s=\frac{{v}_{t}^{2}-{v}_{0}^{2}}{2a}$,可得,$Fs=\frac{1}{2}m{v}_{t}^{2}-\frac{1}{2}m{v}_{0}^{2}$,即外力做功与重物的质量无关,实验不需要测量重物的质量(重力);
(2)该实验中已经测量了物体的位移与速度,来探究合外力与物体的速度的变化关系,所以是否存在摩擦力对该实验没有影响.故不需要平衡摩擦力.
(3)根据表格中记录的数据可得,物体的位移d与物体的速度、以及速度的平方根都不存在正比例的关系,与速度的平方接近正比例关系,所以可选择v2为坐标系的纵坐标.将表格中的数据在d-v2坐标系中描点连线如图.
(4)从图2的图象得到的直接结论是d与v2成正比;从而间接得到做功与物体速度变化的规律是合外力做功与v2成正比.
故答案为:(1)不需要;(2)否;(3)如图;(4)d与v2成正比,做功和速度的二次方成正比.
点评 该实验不同于课本中的实验,这种情况下我们首先要设法理解实验的原理,然后再根据实验的原理进行解答.属于中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图所示,为0.3mol的某种气体的压强和温度关系的p-t图线.p0表示1个标准大气压,则在状态B时气体的体积为( )
如图所示,为0.3mol的某种气体的压强和温度关系的p-t图线.p0表示1个标准大气压,则在状态B时气体的体积为( )
 如图所示,为0.3mol的某种气体的压强和温度关系的p-t图线.p0表示1个标准大气压,则在状态B时气体的体积为( )
如图所示,为0.3mol的某种气体的压强和温度关系的p-t图线.p0表示1个标准大气压,则在状态B时气体的体积为( )| A. | 5.6 L | B. | 3.2 L | C. | 1.2 L | D. | 8.4 L |
11.研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时.假设这种趋势会持续下去,地球的其他条件都不变,未来人类发射的地球同步卫星与现在的相比( )
| A. | 向心加速度变大 | B. | 角速度变大 | ||
| C. | 线速度变大 | D. | 距地面的高度变大 |
18.某同学要测量一电池的电动势和内阻,实验器材有一个电阻箱、一个开关、导线若干和一个自行设计的多用电表.该多用电表的内部结构原理如图1所示,其电流表的量程分别为100mA和1A.
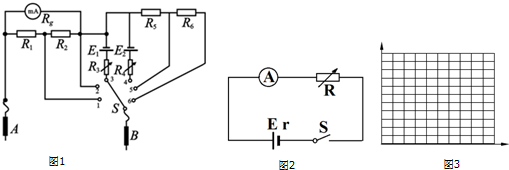
(1)该同学先将选择开关S接“5”,用这个多用电表粗测电池的电动势,则他应该用B表笔连接电池的负极(填“正”或“负”).
(2)接下来该同学使用多用电表的电流档(内阻不计),采用如图2所示的电路进行实验,并得到了表格中数据:
根据表格中数据可知,该同学实验时,多用电表的档位选择开关应接1(填“1”或“2”)
(3)根据表中提供的实验数据,若利用图象确定电池的电动势和内阻,则应作B图象.
A.I-R B.$\frac{1}{I}$-R C.I-$\frac{1}{R}$ D.$\frac{1}{I}-\frac{1}{R}$
(4)根据这些实验数据,在图3坐标纸上做出适当的图线,由做出的图线可知,该电池的电动势是2.3V,内电阻为0.69Ω.

(1)该同学先将选择开关S接“5”,用这个多用电表粗测电池的电动势,则他应该用B表笔连接电池的负极(填“正”或“负”).
(2)接下来该同学使用多用电表的电流档(内阻不计),采用如图2所示的电路进行实验,并得到了表格中数据:
| 实验次数 | 1 | 2 | 3 | 4 | 5 |
| R/Ω | 2 | 4 | 6 | 8 | 10 |
| I/A | 0.83 | 0.46 | 0.31 | 0.24 | 0.19 |
| (1/I)A-1 | 1.20 | 2.19 | 3.20 | 4.21 | 5.20 |
| (1/R)Ω-1 | 0.50 | 0.25 | 0.17 | 0.13 | 0.10 |
(3)根据表中提供的实验数据,若利用图象确定电池的电动势和内阻,则应作B图象.
A.I-R B.$\frac{1}{I}$-R C.I-$\frac{1}{R}$ D.$\frac{1}{I}-\frac{1}{R}$
(4)根据这些实验数据,在图3坐标纸上做出适当的图线,由做出的图线可知,该电池的电动势是2.3V,内电阻为0.69Ω.
15.质量为m的物体,在距地面h高处以$\frac{g}{3}$的加速度由静止竖直下落到地面.下列说法中正确的是( )
| A. | 重力做功$\frac{1}{3}$mgh | B. | 物体的重力势能减少$\frac{1}{3}$mgh | ||
| C. | 物体的动能增加$\frac{1}{3}$mgh | D. | 物体的机械能减少$\frac{1}{3}$mgh |
16.一起重机吊着物体以加速度a(a<g)竖直下落.在下落一段距离的过程中,下列说法中不正确的是( )
| A. | 重力对物体做的功等于物体重力势能的减少量 | |
| B. | 物体重力势能的减少量等于物体动能的增加量 | |
| C. | 重力做的功大于物体克服缆绳的拉力所做的功 | |
| D. | 物体重力势能的减少量大于物体动能的增加量 |
 如图所示,由静止开始被电场(加速电压为U1)加速的带电粒子平行于两正对的平行金属板且从两板正中间射入,从右侧射出,设在此过程中带电粒子没有碰到两极板.若金属板长为L,板间距离为d、两板间电压为U2.
如图所示,由静止开始被电场(加速电压为U1)加速的带电粒子平行于两正对的平行金属板且从两板正中间射入,从右侧射出,设在此过程中带电粒子没有碰到两极板.若金属板长为L,板间距离为d、两板间电压为U2.