题目内容
(2013?保定一模)如图甲所示,有一个大木箱,放在平板汽车的后部,木箱到驾驶室的距离L=2.8m,木箱与车板间的动摩擦因数?=0.5.开始时平板汽车载着木箱以速 度v0=16m/s匀速行驶.突然驾驶员遇到紧急情况刹车,轮胎抱死,使平板汽车做 匀减速直线运动,直至停止.g取10m/s2,忽略空气阻力.
(1)为了不让木箱撞击驾驶室,平板汽车从开始刹车到完全停止至少需多长时间?(计算结果小数点后面保留两位有效数字)
(2)从汽车开始减速到木箱完全停止的过程中,平板汽车受到地面的摩擦力f,在图乙中定性画出f随时间t的变化图线.(不要求写出计算过程,只按画出的 图线评分)

(1)为了不让木箱撞击驾驶室,平板汽车从开始刹车到完全停止至少需多长时间?(计算结果小数点后面保留两位有效数字)
(2)从汽车开始减速到木箱完全停止的过程中,平板汽车受到地面的摩擦力f,在图乙中定性画出f随时间t的变化图线.(不要求写出计算过程,只按画出的 图线评分)

分析:(1)若要木箱和平板车不相碰,则应该有:木箱的位移≤车的位移与L的和,木箱和平板车都是做匀减速直线运动,由此可以列式求出两者位移表达式,进而代入前面的不等式关系进行解题,不等式取等号时时间是最小值.
(1)汽车先受地面的滑动摩擦力,汽车停止到木箱停止的过程汽车受地面的静摩擦力.
(1)汽车先受地面的滑动摩擦力,汽车停止到木箱停止的过程汽车受地面的静摩擦力.
解答:解:(1)设平板车的加速度为a1,车经时间t停定,则:
S车=
对木箱根据运动学公式得:S箱=
对木箱受力分析,根据牛顿第二定律得:
μmg=ma
由题意:S箱-S车=L
联立解得:t=2.85s;
(2)木箱的加速度a=
=5m/s2
木箱停止需要的时间t′=
=3.2s
0-2.85s内汽车受地面的滑动摩擦力f,设此过程汽车的加速度大小为a,
以汽车为研究对象,根据牛顿第二定律:f-μmg=Ma,得:f=Ma+μmg,即f>μmg;
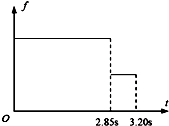
当汽车停止后,木箱仍然前进,根据二力平衡,水平方向汽车受地面的静摩擦力等于受到木箱的滑动摩擦力大小,即f=μmg,故f随时间t的变化图线如图:
答:(1)平板汽车从开始刹车到完全停止至少需2.85s.
(2)f随时间t的变化图线如图.
S车=
| v0t |
| 2 |
对木箱根据运动学公式得:S箱=
| v02 |
| 2a |
对木箱受力分析,根据牛顿第二定律得:
μmg=ma
由题意:S箱-S车=L
联立解得:t=2.85s;
(2)木箱的加速度a=
| μmg |
| m |
木箱停止需要的时间t′=
| 16m/s |
| 5m/s2 |
0-2.85s内汽车受地面的滑动摩擦力f,设此过程汽车的加速度大小为a,
以汽车为研究对象,根据牛顿第二定律:f-μmg=Ma,得:f=Ma+μmg,即f>μmg;
当汽车停止后,木箱仍然前进,根据二力平衡,水平方向汽车受地面的静摩擦力等于受到木箱的滑动摩擦力大小,即f=μmg,故f随时间t的变化图线如图:

答:(1)平板汽车从开始刹车到完全停止至少需2.85s.
(2)f随时间t的变化图线如图.
点评:本题是追及和相遇类问题,若两者不相碰,两者位移关系,应该是后面的小于前面的加两者初始距离.满足这一条件两者不相碰.

练习册系列答案
相关题目
 (2013?保定一模)如图所示,小球A、B质量相同,分别连接在轻质细杆的两端,可绕过细杆中点O的固定水平轴自由转动.现给小球一初速度,使它们做圆周运动,当小球B运动到轨道的最低点时,细杆对小球B的 作用力竖直向上,大小是小球B的重力的2倍;此时小球A 运动到轨道的最高点,则细杆对小球A的作用力是( )
(2013?保定一模)如图所示,小球A、B质量相同,分别连接在轻质细杆的两端,可绕过细杆中点O的固定水平轴自由转动.现给小球一初速度,使它们做圆周运动,当小球B运动到轨道的最低点时,细杆对小球B的 作用力竖直向上,大小是小球B的重力的2倍;此时小球A 运动到轨道的最高点,则细杆对小球A的作用力是( ) (2013?保定一模)如图所示,三个电荷量均为+q的点电荷分别位于等腰直角三角形的三个顶点位 置,a、b、c分别是三角形三条边的中点,以下判断正确的是( )
(2013?保定一模)如图所示,三个电荷量均为+q的点电荷分别位于等腰直角三角形的三个顶点位 置,a、b、c分别是三角形三条边的中点,以下判断正确的是( )