题目内容
如图，小球P、Q的质量相等，其间用轻弹簧相连，光滑斜面倾角为θ，系统静止时，弹簧与轻绳均平行与斜面，则在轻绳被突然剪断的瞬间，下列说法正确的是 （ ）
| A．两球的加速度大小均为gsinθ | B．Q球的加速度为零 |
| C．P球的加速度大小为2gsinθ | D．P球的加速度大小为gsinθ |
BC
解析试题分析：细线剪断前，Q球受弹簧的弹力为：
，轻绳剪断的瞬时，弹簧的弹力不能突变，则Q 受的合外力不变，故加速度为零，选项B正确，A错误；细线剪断前细绳的拉力：
，轻绳剪断的瞬时，细绳的拉力突然变为零，而弹簧的弹力不能突变，故此时P所受的合外力为：
，此时的加速度为：aP=2gsinθ，选项C 正确，D错误。
考点：瞬时态问题；牛顿定律的应用。
练习册系列答案
相关题目
关于惯性的认识，以下说法正确的是
| A．物体受到力的作用后，运动状态发生改变，惯性也随之改变 |
| B．置于光滑水平面上的物体即使质量很大也能被拉动，说明惯性与物体的质量无关 |
| C．让物体的速度发生改变，无论多快，都需要一定时间，这是因为物体具有惯性 |
| D．同一物体沿同一水平面滑动，速度较大时停下的时间较长，说明惯性与速度有关 |
如图所示，长为l的细绳一端固定在O点，另一端拴住一个小球，在O点的正下方与O点相距的地方有一枚与竖直平面垂直的钉子；把小球拉起使细绳在水平方向伸直，由静止开始释放，当细绳碰到钉子的瞬间，下列说法正确的是 （ ）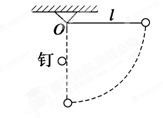
| A．小球的线速度不发生突变 |
| B．小球的角速度突然增大到原来的2倍 |
| C．小球的向心加速度突然增大到原来的2倍 |
| D．绳子对小球的拉力突然增大到原来的2倍 |
如图所示，AB为光滑竖直杆，ACB为构成直角的光滑L形直轨道，C处有一小圆弧连接可使小球顺利转弯（即通过转弯处不损失机械能）。套在AB杆上的小球自A点静止释放，分别沿AB轨道和ACB轨道运动，如果沿ACB轨道运动的时间是沿AB轨道运动时间的1.5倍，则BA与CA的夹角为：（ ）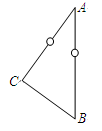
| A．30º | B．45º | C．53º | D．60º |
如图所示，一根轻弹簧下端固定，竖立在水平面上。其正上方A位置有一只小球。小球从静止开始下落，在B位置接触弹簧的上端，在C位置小球所受弹力大小等于重力，在D位置小球速度减小到零。小球下降阶段下列说法中正确的是：
| A．在B位置小球速度最大 |
| B．在C位置小球速度最大 |
| C．从A→C位置小球重力势能的减少量小于重力做的功 |
| D．从A→D位置小球重力势能的减少等于弹簧弹性势能的增加 |
如图所示，在同一竖直平面内有两个正对着的半圆形光滑轨道，轨道的半径都是R.轨道端点所在的水平线相隔一定的距离x.一质量为m的小球能在其间运动而不脱离轨道，经过最低点B时的速度为v.小球在最低点B与最高点A对轨道的压力之差为ΔF（ΔF>0），不计空气阻力．则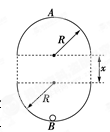 
| A．m、x一定时，R越大，ΔF一定越大 |
| B．m、x一定时，v越大，ΔF一定越大 |
| C．m、R一定时，x越大，ΔF一定越大 |
| D．m、R一定时，v越大，ΔF一定越大 |