Question

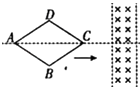
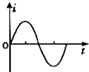
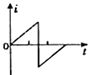
【题目】如图甲所示，A、B是两水平放置的足够长的平行金属板，组成偏转匀强电场，B板接地．A板电势φA随时间变化情况如图乙所示，C、D两平行金属板竖直放置，中间有正对两孔O1′和O2 ， 两板间电压为U2 ， 组成减速电场．现有一带负电粒子在t=0时刻以一定初速度沿AB两板间的中轴线O1O1′进入，并能从O1′沿O1′O2进入C、D间，刚好到达O2孔，已知带电粒子带电荷量为﹣q，质量为m，不计其重力．求：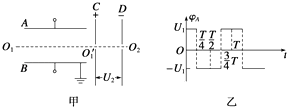
（1）该粒子进入A、B的初速度v0的大小；
（2）A、B两板间距的最小值和A、B两板长度的最小值．

Answer 1

【答案】
（1）解：因粒子在A、B间运动时，水平方向不受外力做匀速运动，所以进入O1′孔的速度即为进入A、B板的初速度．

在C、D间，由动能定理得：qU2= mv02

解得：v0=

答：该粒子进入A、B的初速度v0的大小是 ；

（2）解：由于粒子进入A、B后，在一个周期T内，竖直方向上的速度变为初始状态．即：v竖=0，

若在第一个周期内进入O1′孔，则对应两板最短长度为L=v0T，若在该时间内，粒子刚好不到A板而返回，则对应两板最小间距，设为d．

所以有： a（ ）2×2= ，a=

得：d= = ．

因此A、B两极板间距d的最小值是 ．

答：A、B两板间距的最小值是 ，A、B两板长度的最小值是v0T．

【解析】（1）粒子在AB间运动时，在水平方向不受力，做匀速直线运动，进入O1′孔的速度即为进入A、B板的初速度．研究粒子在CD间运动的过程，运用动能定理求解．（2）粒子在AB间运动时，竖直方向上做周期性的运动，在一个周期T内，竖直方向上的速度变为初始状态；要使该带电粒子能够返回至O1′，应满足在 的整数倍时从CD间出去，根据粒子在匀强电场中的偏转位移公式求出板间距．