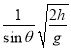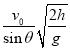题目内容
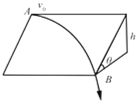
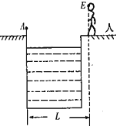
【题目】如图是某研究机构进行带电粒子回收试验的原理图.一群分布均匀的正离子以水平速度![]() 进入水平放置的平行金属板,正离子的比荷
进入水平放置的平行金属板,正离子的比荷![]() ,己知金属板的长度
,己知金属板的长度![]() ,间距为
,间距为![]() ,板间的电势差
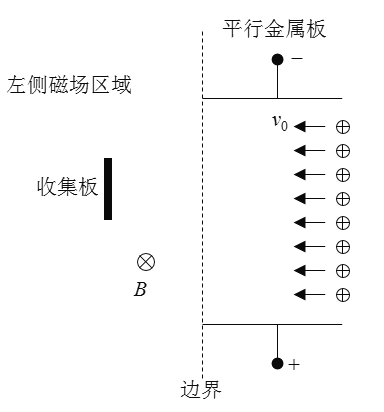
,板间的电势差![]() (下板为高电势).紧靠平行金属板的左侧有一竖直边界,整个左侧区域中都有垂直纸面向内的匀强磁场.边界的左侧区域内有一块竖直放置的电荷收集板(厚度不计),收集板可以在平面内上下左右平移并且长度可以调节,当离子碰到收集板左侧或右侧时会立即被吸收.整个装置置于真空环境中,不考虑离子的重力及离子间的相互作用,忽略离子运动对电场和磁场的影响和极板的边缘效应.
(下板为高电势).紧靠平行金属板的左侧有一竖直边界,整个左侧区域中都有垂直纸面向内的匀强磁场.边界的左侧区域内有一块竖直放置的电荷收集板(厚度不计),收集板可以在平面内上下左右平移并且长度可以调节,当离子碰到收集板左侧或右侧时会立即被吸收.整个装置置于真空环境中,不考虑离子的重力及离子间的相互作用,忽略离子运动对电场和磁场的影响和极板的边缘效应.
(1)求能进入左侧区域的离子在电场中的侧移量![]() ;
;
(2)若没有放罝收集板,要使所有进入左侧区域的离子都能从左侧的竖直边界返回到平行金属板内,求左侧的区域匀强磁场的磁感应强度大小应满足的条件;
(3)若左侧磁场的磁感应强度分别为![]() 、
、![]() ,要使所有进入左侧区域的离子都能被收集板收集,求对应收集板的最短长度
,要使所有进入左侧区域的离子都能被收集板收集,求对应收集板的最短长度![]() .
.
【答案】(1) 0.05m (2) B<0.4T (3) ![]()
![]()
【解析】
由题意可知考查带电粒子在电场、磁场中运动规律,根据类平抛运动、匀速圆周运动的特点分析计算可得.
带电粒子在电场中做类平抛运动,水平方向做匀速直线运动,设运动时间为t,则有
![]()
竖直方向做匀加速直线运动
![]()
(2)
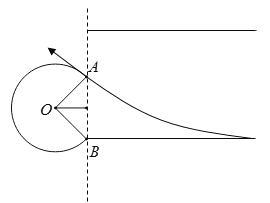
取临界条件分析,从下极板射入磁入的粒子先做类平抛运动,进入磁场后做逆时针方向的匀速圆周运动,
![]()
![]()
设进入磁场时的速度为v,则
![]()
与竖直方向夹角为45°
AB=y=0.05m,由几何关系可求得做匀速圆周运动的半径
![]()
洛伦兹力提供向心力,由牛顿第二定律可得
![]()
联立可得![]()
磁感应强度越大,粒子做圆周运动的半径越小,粒子越能返回到平行金属板,故左侧的区域匀强磁场的磁感应强度大小应满足的条件B<0.4T
(3)由题意可知收集板的最短长度EF的长度,
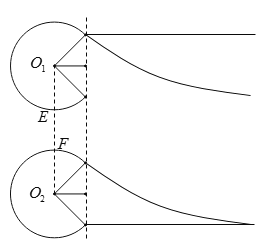
洛伦兹力提供向心力,由牛顿第二定律可得
![]()
代入数值可得![]()
![]()
同理当磁感应强度为B2,可求得
x2=![]()

 名校课堂系列答案
名校课堂系列答案