Question

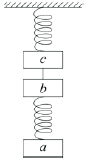
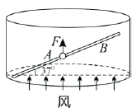
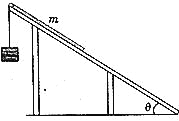
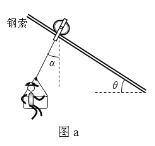
【题目】在不少旅游景点里都设置了一种速降的游乐项目：从山上高处向山下低处安装一根钢索，人坐在吊篮里通过绳索和滑轮沿着倾角为θ的钢索快速下滑，如图a所示。理想情况下，下滑时的加速度大小等于g sin θ，稳定的运动状态下，即滑轮、绳索、人（包括吊篮在内，下同）组成的系统保持相对静止时，绳索与竖直方向间的夹角也等于θ。但实际上有两个原因使得加速度要变小，并且绳索与竖直方向间的夹角一般不等于θ，原因之一是滑轮并非理想的无摩擦，原因之二是空气阻力不能忽略。设滑轮的质量为M，人的质量为m，绳索的质量相对滑轮和人来说可以忽略，滑轮与钢索间的摩擦因数为μ，人运动过程中受到的空气阻力等于人的重力的k倍，滑轮运动过程中受到的空气阻力不计。试通过计算讨论：在稳定的运动状态下，有没有可能绳索与竖直方向间的夹角α＝θ，但加速度的值小于g sin θ？如果有可能，请指出必须满足的条件；如果没有可能，请说明理由。

Answer 1

【答案】只要满足，且μ ≠ 0，k ≠ 0，则α＝θ，且a< g sin θ。

【解析】

有可能α＝θ，且a< g sin θ

滑轮和人（包括吊篮在内）分别看作质点，其受力示意图如图。

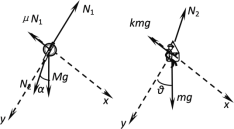
以沿钢索向下为x正方向、垂直钢索向下为y正方向建立平面直角坐标系。分别列牛顿第二定律方程的分量式：

Mg cosθ+N2 cos(θ-α)-N1=0 ①

Mg sinθ+N2 sin(θ-α)-μN1=Ma ②

mg cosθ-N2 cos(θ-α) =0 ③

mg sinθ-N2 sin(θ-α) -kmg=ma ④

解以上四式，得

则只要满足，且μ ≠ 0，k ≠ 0，则α＝θ，且a< g sin θ。