题目内容
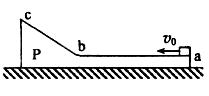
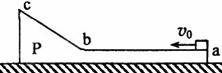
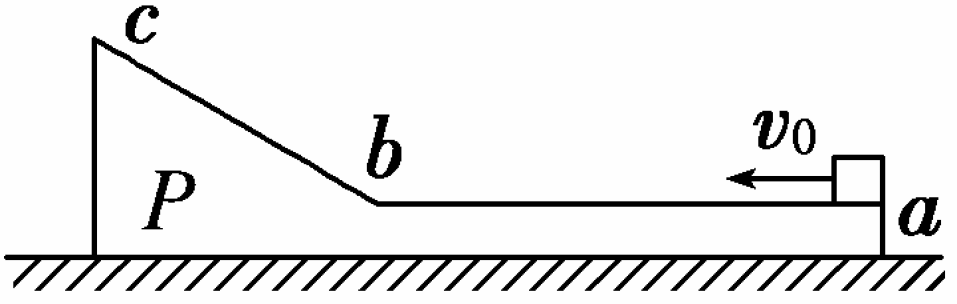
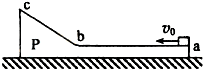
一质量为2m的物体P静止于光滑水地面上，其截面如图所示。图中ab为粗糙的水平面，长度为L；bc为一光滑斜面，斜面和水平面通过与ab与bc均相切的长度可忽略的光滑圆弧连接。现有一质量为m的木块以大小为v0的水平初速度从a点向左运动，在斜面上上升的最大高度为h，返回后在到达a点前与物体P相对静止。重力加速度为g。求：
(1)木块在ab段受到的摩擦力f；
(2)木块最后距a点的距离s。
(1)木块在ab段受到的摩擦力f；
(2)木块最后距a点的距离s。
解：(1)从开始到木块到达最大高度过程：
由动量守恒：mv0＝3mv1
由能的转化及守恒：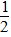
mv02＝
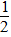3mv12＋mgh＋fL
解得：f＝
(2)从最大高度到最终相对静止：
由动量守恒：3mv1＝3mv2
由能的转化及守恒：
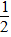3mv12＋mgh＝
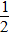3mv22＋fx
距a点的距离：s＝L－x
解得：s＝L－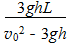
＝
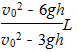
由动量守恒：mv0＝3mv1
由能的转化及守恒：
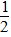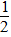mv02＝3mv12＋mgh＋fL解得：f＝
(2)从最大高度到最终相对静止：
由动量守恒：3mv1＝3mv2
由能的转化及守恒：
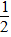3mv12＋mgh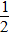＝3mv22＋fx距a点的距离：s＝L－x
解得：s＝L－
＝
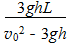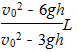
练习册系列答案
期末集结号系列答案
相关题目
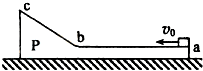一质量为2m的物体P静止于光滑水平地面上，其截面如图所示．图中ab为粗糙的水平面，长度为L；bc为一光滑斜面，斜面和水平面通过与ab和bc均相切的长度可忽略的光滑圆弧连接．现有一质量为m的木块以大小为v0的水平初速度从a点向左运动，在斜面上上升的最大高度为h，返回后在到达a点前与物体P相对静止．重力加速度为g．求：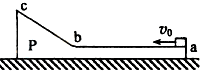
（1）用某种单色光照射某种金属表面，发生了光电效应．现将该单色光的强度减弱，则
