题目内容
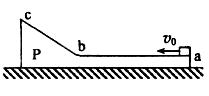
 一质量为2m的物体P静止于光滑水平地面上,其截面如图所示.图中ab为粗糙的水平面,长度为L;bc为一光滑斜面,斜面和水平面通过与ab和bc均相切的长度可忽略的光滑圆弧连接.现有一质量为m的木块以大小为v0的水平初速度从a点向左运动,在斜面上上升的最大高度为h,返回后在到达a点前与物体P相对静止.重力加速度为g.求:
一质量为2m的物体P静止于光滑水平地面上,其截面如图所示.图中ab为粗糙的水平面,长度为L;bc为一光滑斜面,斜面和水平面通过与ab和bc均相切的长度可忽略的光滑圆弧连接.现有一质量为m的木块以大小为v0的水平初速度从a点向左运动,在斜面上上升的最大高度为h,返回后在到达a点前与物体P相对静止.重力加速度为g.求:(1)木块在ab段受到的摩擦力f;
(2)木块最后距a点的距离s.
分析:(1)两物体从开始到第一次到达共同速度过程中动量守恒,结合动量守恒定律和能量守恒定律求出木块在ab段受到的摩擦力.
(2)木块返回与物体P第二次达到共同速度与第一次达到共同的速度相同,对全过程运用能量守恒定律求出木块最后距a点的距离s.
(2)木块返回与物体P第二次达到共同速度与第一次达到共同的速度相同,对全过程运用能量守恒定律求出木块最后距a点的距离s.
解答:解:(1)设木块和物体P共同速度为v,两物体从开始到第一次到达共同速度过程由动量和能量守恒得:mv0=(m+2m)v…①
mv02=
(m+2m)v2+mgh+fL…②
由①②得:f=
…③
(2)木块返回与物体P第二次达到共同速度与第一次相同(动量守恒)全过程能量守恒得:
mv02=
(m+2m)v2+f(2L-s)…④
由②③④得:s=
L.
答:(1)木块在ab段受到的摩擦力f=
.
(2)木块最后距a点的距离s=
L.
| 1 |
| 2 |
| 1 |
| 2 |
由①②得:f=
| m(v02-3gh) |
| 3L |
(2)木块返回与物体P第二次达到共同速度与第一次相同(动量守恒)全过程能量守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
由②③④得:s=
| v02-6gh |
| v02-3gh |
答:(1)木块在ab段受到的摩擦力f=
| m(v02-3gh) |
| 3L |
(2)木块最后距a点的距离s=
| v02-6gh |
| v02-3gh |
点评:本题综合运用了动量守恒定律和能量守恒定律,关键选择研究的过程,根据定律列表达式进行求解.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目

 (1)用某种单色光照射某种金属表面,发生了光电效应.现将该单色光的强度减弱,则
(1)用某种单色光照射某种金属表面,发生了光电效应.现将该单色光的强度减弱,则