题目内容
如下图所示的木板由倾斜部分和水平部分组成,两部分之间由一段圆弧面相连接.在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球,在施加于1号球的水平外力F的作用下均静止,力F与圆槽在同一竖直面内,此时1号球球心距它在水平槽运动时的球心高度差为h.现撤去力F使小球开始运动,直到所有小球均运动到水平槽内.重力加速度为g.求: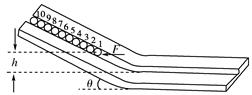
(1)水平外力F的大小;
(2)1号球刚运动到水平槽时的速度;
(3)整个运动过程中,2号球对1号球所做的功.
(1)10mgtan θ (2)  (3)9mgrsin θ
(3)9mgrsin θ
解析试题分析:(1)以10个小球整体为研究对象,由力的平衡条件可得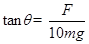
得F=10mgtan θ.
(2)以1号球为研究对象,根据机械能守恒定律可得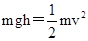 解得
解得
(3)撤去水平外力F后,以10个小球整体为研究对象,利用机械能守恒定律可得: 解得
解得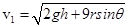
以1号球为研究对象,由动能定理得
得W=9mgrsin θ.
考点:动能定理的应用;共点力平衡的条件及其应用;机械能守恒定律.
点评:本题解题关键有两个:一要选择研究对象,二是明确解题规律.当10个球都在斜面上下滑时,相互间没有作用力,机械能守恒.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
质量为m的小球,从离桌面H高处由静止下落,桌面离地面高度为h,如图所示,若以地面为参考平面,那么小球落地时的重力势能及下落过程中重力势能的变化分别为
| A.mgh,减少mg(H-h) |
| B.mgh,增加mg(H+h) |
| C.-mgh,增加mg(H-h) |
| D.0,减少mg(H+h) |
蹦床运动是运动员从蹦床反弹起来后在空中表演技巧的运动.如图所示.当运动员从最高处下降至最低处的过程中(不计空气阻力),运动员( )
| A.动能一直增大 | B.所受重力始终做正功 |
| C.动能一直减小 | D.重力势能只转变成动能 |
 。
。

 的小球以某一速度从C点运动到A点进入轨道,小球与水平地面间的动摩擦因数为
的小球以某一速度从C点运动到A点进入轨道,小球与水平地面间的动摩擦因数为 。它经过最高点B飞出后又能落回到C点,AC=2R。求小球从C点开始运动时的初速度v0的大小。
。它经过最高点B飞出后又能落回到C点,AC=2R。求小球从C点开始运动时的初速度v0的大小。
 ,方向与x轴正方向相同.在O处放一个电荷量
,方向与x轴正方向相同.在O处放一个电荷量 ,质量
,质量 的绝缘物块.物块与水平面间的动摩擦因数
的绝缘物块.物块与水平面间的动摩擦因数 ,沿x轴正方向给物块一个初速度
,沿x轴正方向给物块一个初速度 ,如上图所示.(g取
,如上图所示.(g取 )试求:
)试求:
