Question

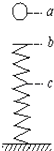
【题目】如图所示，B和C是一组塔轮，即B和C半径不同，但固定在同一转动轴上，其半径之比为RB：RC=3：2，A轮的半径大小与C轮相同，它与B轮紧靠在一起，当A轮绕过其中心的竖直轴转动时，由于摩擦作用，B轮也随之无滑动地转动起来．a、b、c分别为三轮边缘的三个点，则a、b、c三点在运动过程中的（ ）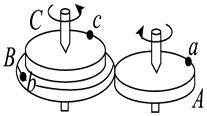

A.线速度大小之比为3：3：2
B.角速度之比为3：3：2
C.转速之比为2：3：2
D.向心加速度大小之比为9：6：4

Answer 1

【答案】A,D
【解析】解：①轮A、轮B靠摩擦传动，边缘点线速度相等，故：

va：vb=1：1

根据公式v=rω，有：

ωa：ωb=3：2

根据ω=2πn，有：

na：nb=3：2

根据a=vω，有：

aa：ab=3：2

②轮B、轮C是共轴传动，角速度相等，故：

ωb：ωc=1：1

根据公式v=rω，有：

vb：vc=3：2

根据ω=2πn，有：

nb：nc=1：1

根据a=vω，有：

ab：ac=3：2

综合得到：

va：vb：vc=3：3：2

ωa：ωb：ωc=3：2：2

na：nb：nc=3：2：2

aa：ab：ac=9：6：4．故AD正确，BC错误

故选：AD

轮A、轮B靠摩擦传动，边缘点线速度相等；轮B、轮C是共轴传动，角速度相等；再结合公式v=rω和a=vω列式分析．