题目内容
【题目】如图所示，一块足够长的木板，放在光滑水平面上，在木板上自左向右并非放有序号是1，2，3，…，n的物体，所有物块的质量均为m，与木板间的动摩擦因数都相同，开始时，木板静止不动，第1，2，3，…，n号物块的初速度分别为是v0，2v0，3v0，…，nv0，方向都向右，木板的质量与所有物块的总质量相等，最终所有物块与木板以共同速度匀速运动.设物块之间均无相互碰撞，木板足够长.试求：
（1）所有物块与木板一起匀速运动的速度vn；
（2）第1号物块与木板刚好相对静止时的速度v1；
（3）通过分析与计算说明第k（k＜n）号物块的最小速度vk
【答案】（1）
（2）
（3）
【解析】在木板上各个物块相对木板运动，都给木板一个向右的摩擦力，因各个物块质量相同，滑动摩擦力都一样，木板在摩擦力的作用下向右加速.由于每个物块的初始速度不同，因而相对木板静止的物块顺序依次是1，2，…，n号，当第一号物块由
到相对木板静止时，其动量变化设为
，则其他各个所有物块在这段时间内的动量变化也都为（f相同，T相同），因木板与所有物块总动量守恒，故可用动量守恒关系求出第1号物块相对木板静止时的速度.
（1）设所有物块都相对木块静止时的速度为vn，因木板与所有物块系统水平方向不受外力，动量守恒，应用：
,又
解得：
（2）设第1号物块相对木板静止时的速度为v1，取木板与物块1为系统一部分，第2号物块到第n号物块为系统另一部分，则
木板和物块1有
2至n号物块有
由动量守恒定律：
解得：
（3）设第k号物块相对木板静止时的速度由vk，则第k号物块速度由kv0减为vk的过程中，序数在第k号物块后面的所有物块动量都减小m(kv0-vk),取木板与序号为1至k号以前的各物块为一部分，则
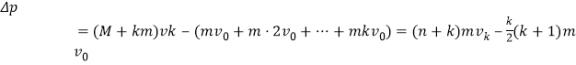
序号在第k以后的所有物块动量减少的总量为：
由动量守恒得
即
。
