题目内容
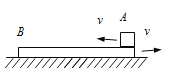
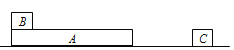
【题目】如图所示，光滑水平轨道上放置长坂A（上表面粗糙）和滑块C，滑块B置于A的左端，三者质量分别为mA=2kg、mB=1kg、mC=2kg。开始时C静止，A、B一起以v0=5m/s的速度匀速向右运动，A与C发生碰撞（时间极短）后C向右运动，经过一段时间A、B再次达到共同速度一起向右运动，且恰好不再与C碰撞。求A与C发生碰撞后瞬间A的速度大小。
【答案】A与C发生碰撞后瞬间A的速度大小是2m/s
【解析】试题分析：因碰撞时间极短，A与C碰撞过程动量守恒，设碰撞后瞬间A的速度大小为vA，C的速度大小为vC，
以向右为正方向，由动量守恒定律得
，①
A与B在摩擦力作用下达到共同速度，设共同速度为vAB，由动量守恒定律得
②
A、B达到共同速度后恰好不再与C碰撞，应满足： 
③，联立①②③式解得：vA=2m/s．
练习册系列答案
相关题目
