题目内容
??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????如图所示,电阻不计的平行金属导轨MN和OP放置在水平面内.MO间接有阻值为R=3Ω的电阻.导轨相距d=lm,其间有竖直向下的匀强磁场,磁感强度B=0.5T.质量为m=0.1kg,电阻为r=lΩ的导体棒CD垂直于导轨放置,并接触良好.用平行于 MN的恒力F=1N向右拉动CD.CD受摩擦阻力f恒为0.5N.求
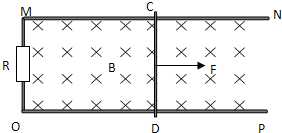
(1)CD运动的最大速度是多少?
(2)当CD到最大速度后,电阻R消耗的电功率是多少?
(3)当CD的速度为最大速度的一半时,CD的加速度是多少?

(1)CD运动的最大速度是多少?
(2)当CD到最大速度后,电阻R消耗的电功率是多少?
(3)当CD的速度为最大速度的一半时,CD的加速度是多少?
分析:(1)导体棒开始做加速度逐渐减小的加速运动,当加速度为零即合外力为零时,速度达到最大.
(2)到达最大速度后,回路中产生稳定感应电流,根据P=I2R可正确求得结果.
(3)当CD的速度为最大速度的一半时,由法拉第电磁感应定律、欧姆定律和安培力公式求出安培力的大小,再由牛顿第二定律求加速度.
(2)到达最大速度后,回路中产生稳定感应电流,根据P=I2R可正确求得结果.
(3)当CD的速度为最大速度的一半时,由法拉第电磁感应定律、欧姆定律和安培力公式求出安培力的大小,再由牛顿第二定律求加速度.
解答:解:(1)设CD棒运动的最大速度为vm,则导体棒产生的感应电动势为:E=Bdvm①
据全电路欧姆定律有:I=
②
则安培力为:F0=BdI ③
据题意分析,当速度最大时,CD棒做匀速直线运动,合力为零,则有:
F-F0-f=0 ④
联立①②③④得:vm=
=8 m/s ⑤
故CD棒运动的最大速度为8m/s.
(2)CD速度最大时,同理有:Em=Bdvm ⑥
Im=
⑦
P=I2R ⑧
联立⑤⑥⑦⑧带入数据得:P=3W.
故当CD达到最大速度后,电阻R消耗的电功率为P=3W.
(3)当CD的速度为最大速度的一半时,有
感应电动势为 E′=
感应电流为 I′=
CD棒所受的安培力为 F′=BId
联立得 F′=
=
N=0.25N
根据牛顿第二定律得 F合=F-F′-f=ma
代入解得:a=2.5m/s2.
答:
(1)CD运动的最大速度为8m/s.
(2)当CD到最大速度后,电阻R消耗的电功率是3W.
(3)当CD的速度为最大速度的一半时,CD的加速度是2.5m/s2.
据全电路欧姆定律有:I=
| E |
| R+r |
则安培力为:F0=BdI ③
据题意分析,当速度最大时,CD棒做匀速直线运动,合力为零,则有:
F-F0-f=0 ④
联立①②③④得:vm=
| (F-f)(R+r) |
| B2d2 |
故CD棒运动的最大速度为8m/s.
(2)CD速度最大时,同理有:Em=Bdvm ⑥
Im=
| Em |
| R+r |
P=I2R ⑧
联立⑤⑥⑦⑧带入数据得:P=3W.
故当CD达到最大速度后,电阻R消耗的电功率为P=3W.
(3)当CD的速度为最大速度的一半时,有
感应电动势为 E′=
| Bdvm |
| 2 |
感应电流为 I′=
| E′ |
| R+r |
CD棒所受的安培力为 F′=BId
联立得 F′=
| B2d2vm |
| 2(R+r) |
| 0.52×12×8 |
| 2×(3+1) |
根据牛顿第二定律得 F合=F-F′-f=ma
代入解得:a=2.5m/s2.
答:
(1)CD运动的最大速度为8m/s.
(2)当CD到最大速度后,电阻R消耗的电功率是3W.
(3)当CD的速度为最大速度的一半时,CD的加速度是2.5m/s2.
点评:本题的难点是对导体棒正确受力分析,弄清其运动情况,得出速度最大的条件,注意对于变加速运动往往合外力为零时对应着速度最大.

练习册系列答案
相关题目
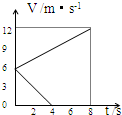 质量为0.8kg的物体在一水平面上运动,如图所示的两条直线分别表示物体受到水平拉力作用和不受拉力作用的V-t图线,该物体所受到的水平拉力是多少?
质量为0.8kg的物体在一水平面上运动,如图所示的两条直线分别表示物体受到水平拉力作用和不受拉力作用的V-t图线,该物体所受到的水平拉力是多少? 如图所示,一质量为M,长为L的木板固定在光滑水平面上.一质量为m的小滑块以水平速度v0从木板的左端开始滑动,滑到木板的右端时速度恰好为零.
如图所示,一质量为M,长为L的木板固定在光滑水平面上.一质量为m的小滑块以水平速度v0从木板的左端开始滑动,滑到木板的右端时速度恰好为零.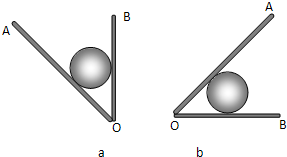 如图(a)所示,小球放置在光滑V形槽中,初始槽板OB处竖直平面,将V形槽沿顺时针绕槽底角O点缓慢转动90°,到OB处水平平面,如图(b)所示.在这个过程中,板OB受到的压力将
如图(a)所示,小球放置在光滑V形槽中,初始槽板OB处竖直平面,将V形槽沿顺时针绕槽底角O点缓慢转动90°,到OB处水平平面,如图(b)所示.在这个过程中,板OB受到的压力将 如图所示是用闪光照相法,拍照的一个平抛小球的照片,照相机每隔相等时间曝光一次,请用合理的办法确定重力加速度方向(保留作图痕迹并简要说明),若最高点为水平抛出点,为求得小球平抛的初速度,请在图中标出需测量的线段,并用符号表示.则小球平抛的初速度大小为
如图所示是用闪光照相法,拍照的一个平抛小球的照片,照相机每隔相等时间曝光一次,请用合理的办法确定重力加速度方向(保留作图痕迹并简要说明),若最高点为水平抛出点,为求得小球平抛的初速度,请在图中标出需测量的线段,并用符号表示.则小球平抛的初速度大小为 一列波在介质中向某一方向传播,如图所示为此波在某一时刻的波形图,并且此时振动还只发生在M、N之间,已知此波的周期为T,Q质点速度方向在波形图中是向下的,下面说法中正确的是( )
一列波在介质中向某一方向传播,如图所示为此波在某一时刻的波形图,并且此时振动还只发生在M、N之间,已知此波的周期为T,Q质点速度方向在波形图中是向下的,下面说法中正确的是( ) 在均匀介质中,所示各质点的平衡位置在同一直线上,相邻两质点间的距离为a,振动由质点1向右传播,质点1开始振动的速度方向竖直向上,经时间t,前13个质点第一次形成如图所示的波形,该波的周期为
在均匀介质中,所示各质点的平衡位置在同一直线上,相邻两质点间的距离为a,振动由质点1向右传播,质点1开始振动的速度方向竖直向上,经时间t,前13个质点第一次形成如图所示的波形,该波的周期为 如图所示的装置,U1是加速电压,紧靠其右侧的是两块彼此平行的水平金属板.板长为L,两板间距离为d,一个质量为m、带电量为-q的粒子,经加速电压加速后沿金属板中心线水平射人两板中,若两水平金属板间加一电压U2,当上板为正时,带电粒子恰好能沿两板中心线射出;当下板为正时,带电粒子则射到下板上距板的左端
如图所示的装置,U1是加速电压,紧靠其右侧的是两块彼此平行的水平金属板.板长为L,两板间距离为d,一个质量为m、带电量为-q的粒子,经加速电压加速后沿金属板中心线水平射人两板中,若两水平金属板间加一电压U2,当上板为正时,带电粒子恰好能沿两板中心线射出;当下板为正时,带电粒子则射到下板上距板的左端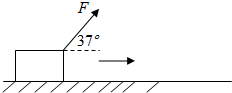 如图所示,一个质量为m=2㎏的物体,受到与水平方向成37°角斜向上方的拉力F1=10N作用,在水平地面上移动了距离x1=2m后撤去拉力,此后物体又滑行了x2=3m的距离后停止了运动.设物体与地面间的滑动摩擦力为它们间弹力的0.2倍,求:(sin37°=0.6,cos37°=0.8)
如图所示,一个质量为m=2㎏的物体,受到与水平方向成37°角斜向上方的拉力F1=10N作用,在水平地面上移动了距离x1=2m后撤去拉力,此后物体又滑行了x2=3m的距离后停止了运动.设物体与地面间的滑动摩擦力为它们间弹力的0.2倍,求:(sin37°=0.6,cos37°=0.8)