��Ŀ����
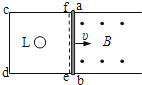
����Ŀ����ͼ��ʾ���⻬б�����Ϊ�ȣ��˹̶�һ��ֱ��б��ĵ���C����б���Ϸ��ó�ľ��A��A���¶���C�ľ���Ϊd��A���϶˷���С���B������Ϊ�ʵ㣩��A��B������ȣ�A��B��Ķ�Ħ��������=1.5tan�ȣ���ͬʱ�ɾ�ֹ�ͷ�A��B��A��C������ײ��ʱ�伫�̣���ײǰ���ٶȴ�С��ȣ������෴���˶������У�С���ʼ��û�д�ľ���ϻ��䣬��֪�������ٶ�Ϊg����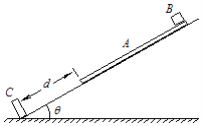
��1��A��C������һ����ײǰ˲����ٶȴ�Сv1��
��2��A��C������һ����ײ���ϻ�����ߵ�ʱ��С�����ٶȴ�Сv2��
��3��ΪʹB����C��ײ��ľ��A���ȵ���СֵL��
���𰸡�
��1��
�⣺��һ����ײǰ�ɻ�е���غ㶨���У� ![]() ��m+m��v12=2mgdsin��
��m+m��v12=2mgdsin��
��ã�v1= ![]()
�� A��C������һ����ײǰ˲����ٶȴ�СΪ ![]() ��
��
��2��
�⣺�跢����һ����ײ��A�ϻ���B�»��ļ��ٶȴ�С�ֱ�ΪaA��aB������ţ�ٵڶ������У�
��ľ��A����mgcos��+mgsin��=maA
��С���B����mgcos�ȩ�mgsin��=maB
����aA��aB����A�ȼ��ٵ��㣬��A��һ����ײ���ϻ�����ߵ��ʱ��Ϊt����
v1=aAt v2=v1��aBt
������ã�v2= ![]()
��A��C������һ����ײ���ϻ�����ߵ�ʱ��С�����ٶȴ�СΪ ![]() ��
��
��3��
�⣺����A��B�˶�ȫ���̣��������غ㶨���У�
mgdsin��+mg��d+L��sin��=��mgLcos��
��ã�L=4d
��ΪʹB����C��ײ��ľ��A���ȵ���СֵΪ4d��
����������1��ABһ���»��Ĺ����У�ֻ������������ϵͳ�Ļ�е���غ㣬�ݴ���ʽ���A��C������һ����ײǰ˲����ٶȴ�Сv1����2��ľ������ʱ����A��B�ֱ�������ţ���˶�������ʽ�����ٶȣ��ɵõ�A�ļ��ٶȴ���B�ļ��ٶȴ�С��˵��A���ٶ��ȼ����㣮���ٶ�ʱ�乫ʽ���v2����3�����ڲ��ϵ��ϻ�����ײ������A��Bǡ�ö�ͣ��C��ʱ����ȫ���̣����������غ����L����Сֵ��
�����㾫����������Ҫ�����˶��ܶ������ۺ�Ӧ�úͻ�е���ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ����Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�ϵͳ��̬���ܻ�е��E 1 ����ĩ̬���ܻ�е��E 2 ����E1 =E2��ϵͳ���ٵ����������ܦ�E P�� ����ϵͳ���ӵ��ܶ��ܦ�E K�� ������E P�� =��E K������ϵͳֻ��A��

 ��У����ϵ�д�
��У����ϵ�д�