题目内容
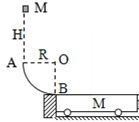
【题目】如图所示，两竖直虚线间距为L，之间存在竖直向下的匀强电场。自该区域的A点将质量为m、电荷量分别为q和－q(q>0)的带电小球M、N先后以相同的初速度沿水平方向射出。小球进入电场区域，并从该区域的右边界离开。已知N离开电场时的位置与A点在同一高度；M刚离开电场时的动能为刚进入电场时动能的8倍。不计空气阻力，重力加速度大小为g。已知A点到左边界的距离也为L。
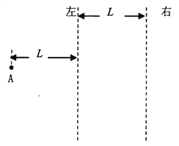
（1）求该电场的电场强度大小；
（2）求小球射出的初速度大小；
（3）要使小球M、N离开电场时的位置之间的距离不超过L，仅改变两小球的相同射出速度，求射出速度需满足的条件。
【答案】（1）
（2）
（3）
【解析】小球运动过程只受重力和电场力作用，故小球在水平方向做匀速运动，那么，小球在电场区域内外的运动时间t相同；在电场区域外，小球在竖直方向做加速度为g的匀加速运动，故小球进入电场时的竖直分速度为
；
（1）N离开电场时的位置与A点在同一高度，即竖直位移为零；设N在电场内的加速度为a，则有：
，所以，
，方向竖直向上；
故由牛顿第二定律可得
，所以电场的电场强度
；
（2）M在电场中的加速度
，方向竖直向下；
故M刚离开电场时的竖直分速度
；
又有小球在水平方向做匀速运动，设小球射出的初速度为v0，则有：
；
故由M刚离开电场时的动能为刚进入电场时动能的8倍可得：
；
所以
，
所以
，所以；
（3）M、N进入电场前的运动一致，那么，M、N离开电场时的位置之间的距离
，
故
；又有，
所以
；
练习册系列答案
阅读快车系列答案
相关题目
