题目内容
10.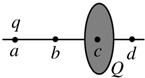 如图所示,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心c的轴线上有a、b、d三个点,a和b、b和c、c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则d点处场强的大小为$\frac{10kq}{{9R}^{2}}$(k为静电力常量).
如图所示,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心c的轴线上有a、b、d三个点,a和b、b和c、c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则d点处场强的大小为$\frac{10kq}{{9R}^{2}}$(k为静电力常量).
分析 由题意可知,半径为R均匀分布着电荷量为Q的圆盘上电荷,与在a点处有一电荷量为q(q>0)的固定点电荷,在b点处的场强为零,说明各自电场强度大小相等,方向相反.那么在d点处场强的大小即为两者之和.因此根据点电荷的电场强度为E=k$\frac{q}{{R}^{2}}$即可求解
解答 解:电荷量为q的点电荷在b处产生电场强度为:E=k$\frac{q}{{R}^{2}}$,而半径为R均匀分布着电荷量为Q的圆盘上电荷,与在a点处有一电荷量为q(q>0)的固定点电荷,在b点处的场强为零,则圆盘在此处产生电场强度也为:E=k$\frac{q}{{R}^{2}}$.
那么圆盘在此d产生电场强度则仍为:E=k$\frac{q}{{R}^{2}}$.
而电荷量为q的点电荷在d处产生电场强度为:E′=k$\frac{q}{{(3R)}^{2}}$=k$\frac{q}{{9R}^{2}}$,由于都在d处产生电场强度方向相同,即为两者大小相加.
所以两者这d处产生电场强度为$\frac{10kq}{{9R}^{2}}$.
故答案为:$\frac{10kq}{{9R}^{2}}$
点评 考查点电荷与圆盘电荷在某处的电场强度叠加,紧扣电场强度的大小与方向关系,从而为解题奠定基础.

练习册系列答案
相关题目
1.静止的列车在平直的轨道上以恒定功率启动,设阻力不变,在开始的一小段时间内,列车( )
| A. | 受到的牵引力逐渐增大 | B. | 加速度逐渐增大 | ||
| C. | 合外力的瞬时功率逐渐增大 | D. | 克服阻力做功的功率逐渐增大 |
15.下列说法不正确的是( )
| A. | 超声波被血流反射回来其频率发生变化可测血流速度,这是利用多普勒效应 | |
| B. | 空间中某个区域有变化的电场或变化的磁场,不一定能产生电磁波 | |
| C. | 部队过桥不能齐步走而要便步走,是为了避免桥梁发生共振现象 | |
| D. | 用标准平面来检查光学面的平整程度是利用光的衍射现象 |
2.某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图所示,每两个相邻的计数点之间还有4个打印点未画出.

(1)试根据纸带上各个计数点间的距离,计算出打下B点时小车的瞬时速度,并将这个速度值填入下表(要求保留3位有效数字).
(2)由以上数据可求得小车加速度为0.80m/s2.(保留2位小数)

(1)试根据纸带上各个计数点间的距离,计算出打下B点时小车的瞬时速度,并将这个速度值填入下表(要求保留3位有效数字).
| 速度 | vB | vC | vD | vE |
| 数值(m/s) | 0.479 | 0.560 | 0.640 |
19.为了测定电源电动势E的大小、内电阻r和定值电阻R0的阻值,某同学利用DIS设计了如图甲所示的电路.闭合电键S1,调节滑动变阻器的滑动触头P向某一方向移动时,用电压传感器1、电压传感器2和电流传感器测得数据,并根据测量数据计算机分别描绘了如图乙所示的M、N两条U-I直线.请回答下列问题:
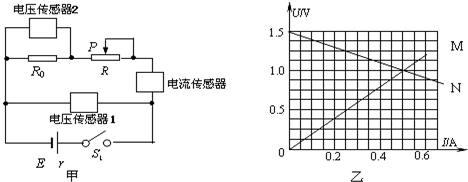
(1)根据图乙中的M、N两条直线可知BC
A.直线M是根据电压传感器1和电流传感器的数据画得的
B.直线M是根据电压传感器2和电流传感器的数据画得的
C.直线N是根据电压传感器1和电流传感器的数据画得的
D.直线N是根据电压传感器2和电流传感器的数据画得的
(2)图象中两直线交点处电路中的工作状态是ABC
(3)根据图乙可以求得定值电阻R0=2.0Ω,电源电动势E=1.50V,内电阻r=1.0Ω.

(1)根据图乙中的M、N两条直线可知BC
A.直线M是根据电压传感器1和电流传感器的数据画得的
B.直线M是根据电压传感器2和电流传感器的数据画得的
C.直线N是根据电压传感器1和电流传感器的数据画得的
D.直线N是根据电压传感器2和电流传感器的数据画得的
(2)图象中两直线交点处电路中的工作状态是ABC
| A.滑动变阻器的滑动头P滑到了最左端 | B.该电源在该电路中的输出功率最大 |
| C.定值电阻R0上消耗的功率为0.5W | D.该电源在该电路中的效率达到最大值 |
20.某物体做匀加速直线运动,加速度大小为a,速度变化量为△v,发生位移为x,紧接着速度变化为同样的△v发生的位移为( )
| A. | x-$\frac{(△v)^2}{2a}$ | B. | x+$\frac{(△v)^2}{2a}$ | C. | x-$\frac{(△v)^2}{a}$ | D. | x+$\frac{(△v)^2}{a}$ |