题目内容
1.将一天的时间记为T,地面上的重力加速度记为g,地球半径记为R(1)试求地球同步卫星P的轨道半径rp
(2)一卫星Q位于赤道上空,赤道一城市A的人每天看到两次卫星Q掠过上空,求Q的轨道半径.假设卫星运动方向与地球自转方向相同.
分析 (1)由万有引力等于向心力列出等式求解轨道半径
(2)卫星绕地球做匀速圆周运动,赤道一城市A的人每天看到两次卫星Q掠过上空,求出周期关系,由万有引力等于向心力列出等式求解Q的轨道半径.
解答 解:(1)设地球质量为M,同步卫星质量为m,同步卫星周期等于T,由万有引力等于向心力得:
$G\frac{Mm}{{r}_{P}^{2}}=m{r}_{P}{(\frac{2π}{T})}^{2}$
又:$G\frac{Mm}{{R}_{\;}^{2}}=mg$,
联立解得:rP=$\root{3}{\frac{g{R}_{\;}^{2}{T}_{\;}^{2}}{4{π}^{2}}}$.
(2)根据题述,卫星Q的周期T1<T.假设每隔t时间看到一次:
则$\frac{t}{{T}_{1}}-\frac{t}{T}=1$,
考虑到每天看到两次的稳定状态,则有:$t=\frac{1}{2}T$,
解得:${T}_{1}=\frac{1}{3}T$.
对于卫星Q,轨道半径为r,又有:
$\frac{GMm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}_{1}{\;}^{2}}r$.
解得:$r=\root{3}{\frac{g{R}_{\;}^{2}{T}_{\;}^{2}}{36{π}^{2}}}$.
答:(1)地球同步卫星P的轨道半径是$\root{3}{\frac{g{R}_{\;}^{2}{T}_{\;}^{2}}{4{π}^{2}}}$;
(2)Q的轨道半径是$\root{3}{\frac{g{R}_{\;}^{2}{T}_{\;}^{2}}{36{π}^{2}}}$
点评 解决本题的关键知道同步卫星的特点,掌握万有引力提供向心力和万有引力等于重力这两个理论,并能熟练运用.

 名校课堂系列答案
名校课堂系列答案 如图所示,跳水运动员站在3m板的前端静止不动时,关于“运动员受到板对他的弹力方向”,下列说法正确的是( )
如图所示,跳水运动员站在3m板的前端静止不动时,关于“运动员受到板对他的弹力方向”,下列说法正确的是( )| A. | 斜向左上 | B. | 斜向右上 | C. | 竖直向上 | D. | 竖直向下 |
| A. | 物体的加速度是6m/s2 | B. | 物体的初速度是3 m/s | ||
| C. | 前3s内的平均速度13m/s | D. | 第6s末的速度是40m/s |
| A. | 金属 | B. | 电解液 | C. | 气体 | D. | 任何物质 |
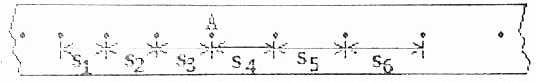 ①则A点瞬时速度的大小为0.850m/s
①则A点瞬时速度的大小为0.850m/s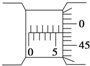 某实验小组在利用单摆测定当地重力加速度的实验中:
某实验小组在利用单摆测定当地重力加速度的实验中:
 如图所示,两个可视为质点的金属小球A、B质量都是m、带正电电荷量都是q,连接小球的绝缘细线长度都是l,静电力常量为k,重力加速度为g.则连结A、B的细线中的张力为多大?连结O、A的细线中的张力为多大?
如图所示,两个可视为质点的金属小球A、B质量都是m、带正电电荷量都是q,连接小球的绝缘细线长度都是l,静电力常量为k,重力加速度为g.则连结A、B的细线中的张力为多大?连结O、A的细线中的张力为多大?