题目内容
13.将80N的力分解,其中一个分力F1与它的夹角为30度.(1)当另一个分力F2最小时求F1的大小;
(2)当F2=50N时求F1的大小.
分析 (1)因为分力和合力构成矢量三角形,当分力F2与分力F1垂直时,F2最小.
(2)F2=50N时,小于合力80N,根据三角形定则可以判断此时F1的大小情况.
解答 解:(1)因为垂直段最短,知当分力F2与分力F1垂直时,F2最小.如图.
则F2时最小值为:F2=Fsin30°=80×$\frac{1}{2}$N=40N.
此时F1的大小为F1=$\sqrt{{F}^{2}-{F}_{2}^{2}}$=$\sqrt{8{0}^{2}-4{0}^{2}}$N=40$\sqrt{3}$N,
(2)当F2=50N时,根据三角形定则可知,F1的大小有两种情况,如图.
根据三角形的边角关系可得,此时F1的大小为(40$\sqrt{3}$-30)N或(40$\sqrt{3}$+30)N;
答:(1)F2最小时另一个分力F1的大小为40$\sqrt{3}$N;
(2)F2=50N时F1的大小为(40$\sqrt{3}$-30)N或(40$\sqrt{3}$+30)N.
点评 解决本题的关键知道合力与分力遵循平行四边形定则(三角形定则),根据作图法可以确定力的最小值,注意第2问题的两种情况是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图所示,一轻杆一端固定在O点,另一端固定一小球,小球在竖直平面内做圆周运动,关于轻杆的形变量与小球的速度大小的关系,下列说法正确的是( )
如图所示,一轻杆一端固定在O点,另一端固定一小球,小球在竖直平面内做圆周运动,关于轻杆的形变量与小球的速度大小的关系,下列说法正确的是( )
 如图所示,一轻杆一端固定在O点,另一端固定一小球,小球在竖直平面内做圆周运动,关于轻杆的形变量与小球的速度大小的关系,下列说法正确的是( )
如图所示,一轻杆一端固定在O点,另一端固定一小球,小球在竖直平面内做圆周运动,关于轻杆的形变量与小球的速度大小的关系,下列说法正确的是( )| A. | 小球在最高点时的速度越大,轻杆的形变量越小 | |
| B. | 小球在最高点时的速度越大,轻杆的形变量越大 | |
| C. | 小球在最低点时的速度越大,轻杆的形变量越小 | |
| D. | 小球在最低点时的速度越大,轻杆的形变量越大 |
18.在下列现象之中,可以证明光是一种波的是( )
| A. | 双缝干涉 | B. | 单缝衍射 | C. | 棱镜色散 | D. | 薄膜干涉 | ||||
| E. | 海市蜃楼 |
2. 四颗人造卫星a、b、c、d在地球大气层外的圆形轨道上运行,其中a、c的轨道半径相同,b、d在同一个圆轨道上,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示,则( )
四颗人造卫星a、b、c、d在地球大气层外的圆形轨道上运行,其中a、c的轨道半径相同,b、d在同一个圆轨道上,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示,则( )
 四颗人造卫星a、b、c、d在地球大气层外的圆形轨道上运行,其中a、c的轨道半径相同,b、d在同一个圆轨道上,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示,则( )
四颗人造卫星a、b、c、d在地球大气层外的圆形轨道上运行,其中a、c的轨道半径相同,b、d在同一个圆轨道上,b、c轨道在同一平面上.某时刻四颗卫星的运行方向及位置如图所示,则( )| A. | 卫星a、c的加速度大小相等,且大于b的加速度 | |
| B. | 卫星b、c的线速度大小相等,且小于a的线速度 | |
| C. | 卫星d通过加速就可追上卫星b | |
| D. | 若卫星c变轨后在轨道半径较大的轨道上做匀速圆周运动,则其周期变大 |
3. 如图所示,电路中R1,R2均为可变电阻,电源内阻不能忽略,平行板电容器C的极板水平放置.闭合电键电路达到稳定时,带电油滴悬浮在两板之间静止不动.如果仅改变下列某一个条件,以下说法正确的是( )
如图所示,电路中R1,R2均为可变电阻,电源内阻不能忽略,平行板电容器C的极板水平放置.闭合电键电路达到稳定时,带电油滴悬浮在两板之间静止不动.如果仅改变下列某一个条件,以下说法正确的是( )
 如图所示,电路中R1,R2均为可变电阻,电源内阻不能忽略,平行板电容器C的极板水平放置.闭合电键电路达到稳定时,带电油滴悬浮在两板之间静止不动.如果仅改变下列某一个条件,以下说法正确的是( )
如图所示,电路中R1,R2均为可变电阻,电源内阻不能忽略,平行板电容器C的极板水平放置.闭合电键电路达到稳定时,带电油滴悬浮在两板之间静止不动.如果仅改变下列某一个条件,以下说法正确的是( )| A. | 减小R1的阻值,油滴向下运动 | B. | 增大R2的阻值,油滴向下运动 | ||
| C. | 断开电键K1,油滴仍静止不动 | D. | 断开电键K2,油滴仍静止不动 |
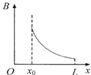
 如图所示,在xOy平面内有一长为L的金属矩形线框abcd,在空间存在着垂直于xOy平面向里的磁场,磁场的磁感应强度的大小只随x值而变化.初始时线框的bc边与y轴重合.现从静止开始用恒定拉力拉着线框通过磁场,若线框在进入磁场区域的最初一段距离L内,线框做匀加速运动,则在x0≤x≤L(其中x0=$\frac{L}{4}$)的范围内磁感应强度大小B随x变化关系图最接近( )
如图所示,在xOy平面内有一长为L的金属矩形线框abcd,在空间存在着垂直于xOy平面向里的磁场,磁场的磁感应强度的大小只随x值而变化.初始时线框的bc边与y轴重合.现从静止开始用恒定拉力拉着线框通过磁场,若线框在进入磁场区域的最初一段距离L内,线框做匀加速运动,则在x0≤x≤L(其中x0=$\frac{L}{4}$)的范围内磁感应强度大小B随x变化关系图最接近( )