题目内容
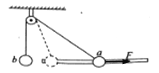
【题目】如图所示,在足够高的光滑、绝缘水平高台边缘,静置一个不带电的小金属块B,另有一与B完全相同的带电量为+q的小金属块A以初速度v0向B运动,A、B的质量均为m。A与B相碰撞后,两物块立即粘在一起,并从台上飞出。已知在高台边缘的右侧空间中存在水平向左的匀强电场,场强大小E=2mg/q。求:(1)A、B一起运动过程中距高台边缘的最大水平距离。 (2)从开始到A、B运动到距高台边缘最大水平距离的过程 A的机械能减少了多少?
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由动量守恒定律求出碰撞后的速度,离开平台后,AB在水平方向做匀减速直线运动,应用牛顿第二定律与运动学公式求出最大距离;
(2)求出碰撞过程损失的机械能,求出离开平台后损失的机械能,然后求出损失的总机械能。
(1) A、B碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:
mυ0=2mυ…①
碰后水平方向:qE=2max…②
![]() …③
…③
由速度位移公式得:0-υ2=-2axXm…④
由①②③④解得:![]() ;
;
(2) )由能量守恒定律可知,碰撞过程中A损失的机械能:
![]()
碰后到距平台边缘最大水平距离的过程中A损失的机械能:
![]()
从A、B碰撞前到A、B运动到距离平台边缘最大水平距离的过程中A损失的机械能为:
![]() 。
。

练习册系列答案
相关题目