题目内容
3. 如图所示,AOB是光滑水平轨道,BC是半径为R的光滑的$\frac{1}{4}$固定圆弧轨道,两轨道恰好相切.质量为M=3m的小木块静止在O点,一个质量为m的子弹以某一初速度水平向右射入小木块内,并留在其中和小木块一起运动.且恰能到达圆弧轨道的最高点C(木块和子弹均可以看成质点).
如图所示,AOB是光滑水平轨道,BC是半径为R的光滑的$\frac{1}{4}$固定圆弧轨道,两轨道恰好相切.质量为M=3m的小木块静止在O点,一个质量为m的子弹以某一初速度水平向右射入小木块内,并留在其中和小木块一起运动.且恰能到达圆弧轨道的最高点C(木块和子弹均可以看成质点).①求子弹射入木块前的速度.
②若每当小木块返回到O点或停止在O点时,立即有相同的子弹射入小木块,并留在其中,则当第5颗子弹射入小木块后,小木块沿圆弧轨道能上升的最大高度为多少?
分析 (1)第一颗子弹射入木块的过程,系统动量守恒,以子弹的初速度方向为正方向,由动量守恒定律与机械能守恒定律可以求出初速度;
(2)由动量守恒定律与机械能守恒定律求出最大高度.
解答 解:(1)第一颗子弹射入木块的过程,系统动量守恒,以子弹的初速度方向为正方向,由动量守恒定律得:
mv0=(m+M)v1,
系统由O到C的运动过程中机械能守恒,由机械能守恒定律得:$\frac{1}{2}$(m+M)v12=(m+M)gR,
已知:M=3m,
解得:v0=$4\sqrt{2gR}$;
(2)由动量守恒定律可知,第2、4、6…颗子弹射入木块后,木块的速度为0,第1、3、5…颗子弹射入后,木块运动.当第5颗子弹射入木块时,以子弹初速度方向为正方向,由动量守恒定律得:
mv0=(5m+M)v5,
设此后木块沿圆弧上升的最大高度为H,由机械能守恒得:
$\frac{1}{2}$(5m+M)v52=(5m+M)gH,
由以上各式可得:H=$\frac{1}{4}$R;
答:(1)子弹射入木块前的速度为$4\sqrt{2gR}$.
(2)若每当小木块返回到O点或停止在O点时,立即有相同的子弹射入小木块,并留在其中,则当第5颗子弹射入小木块后,小木块沿圆弧轨道能上升的最大高度为$\frac{1}{4}$R.
点评 本题考查了求速度与木块上升的高度问题,分析清楚物体运动过程、应用动量守恒定律与机械能守恒定律即可正确解题.

练习册系列答案
相关题目
18.一质量为1kg的物体被人用手由静止向上提升1m,这时物体的速度是2m/s,则下列说法中正确的是(g取10m/s2)( )
| A. | 手对物体作功10 J | B. | 合外力对物体作功12 J | ||
| C. | 合外力对物体作功2 J | D. | 物体克服重力作功5 J |
15.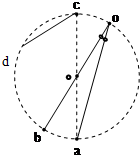 如图所示,oa、ob、cd是竖直平面内三根固定的光滑细杆,o、a、b、c、d位于同一圆周上,c为圆周的最高点,a为最低点.每根杆上都套着一个小滑环,三个滑环从o点或c点无初速释放,用t1、t2、t3分别表示滑环到达a、b、d点所用的时间,则下列关系正确的是( )
如图所示,oa、ob、cd是竖直平面内三根固定的光滑细杆,o、a、b、c、d位于同一圆周上,c为圆周的最高点,a为最低点.每根杆上都套着一个小滑环,三个滑环从o点或c点无初速释放,用t1、t2、t3分别表示滑环到达a、b、d点所用的时间,则下列关系正确的是( )
 如图所示,oa、ob、cd是竖直平面内三根固定的光滑细杆,o、a、b、c、d位于同一圆周上,c为圆周的最高点,a为最低点.每根杆上都套着一个小滑环,三个滑环从o点或c点无初速释放,用t1、t2、t3分别表示滑环到达a、b、d点所用的时间,则下列关系正确的是( )
如图所示,oa、ob、cd是竖直平面内三根固定的光滑细杆,o、a、b、c、d位于同一圆周上,c为圆周的最高点,a为最低点.每根杆上都套着一个小滑环,三个滑环从o点或c点无初速释放,用t1、t2、t3分别表示滑环到达a、b、d点所用的时间,则下列关系正确的是( )| A. | t1=t2 | B. | t1>t2 | C. | t3<t2 | D. | t1<t3 |
12.下列说法正确的是( )
| A. | 曲线运动可以是匀变速运动 | B. | 曲线运动的加速度可能为零 | ||
| C. | 做曲线运动的物体加速度一定变化 | D. | 匀速率圆周运动是匀变速运动 |
13.一物体做匀变速直线运动,某时刻速度的大小为4m/s,1s后速度的大小变为10m/s,在这1s内该物体的( )
| A. | 位移的大小可能小于4 m | B. | 加速度的大小可能大于10 m/s2 | ||
| C. | 加速度的大小可能小于4 m/s2 | D. | 位移的大小可能大于10 m |
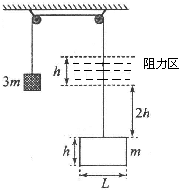 如图所示,质量为3m的重物与一质量为m的矩形线框用一根轻质细线连接起来,挂在两个高度相同的定滑轮上,已知线框竖直边长为h,横边边长为L.在线框正上方2h处有一阻力区,阻力区宽度为h,足够长,在线框穿越过程中可提供一大小与速度成正比的阻力:f=kv(k为已知量).将重物从静止开始释放,线框加速进入阻力区,穿出阻力区前已经做匀速直线运动,滑轮质量、摩擦阻力均不计,重力加速度为g.试求:
如图所示,质量为3m的重物与一质量为m的矩形线框用一根轻质细线连接起来,挂在两个高度相同的定滑轮上,已知线框竖直边长为h,横边边长为L.在线框正上方2h处有一阻力区,阻力区宽度为h,足够长,在线框穿越过程中可提供一大小与速度成正比的阻力:f=kv(k为已知量).将重物从静止开始释放,线框加速进入阻力区,穿出阻力区前已经做匀速直线运动,滑轮质量、摩擦阻力均不计,重力加速度为g.试求: 在如图所示的并联电路中,保持干路上的电流I不变,当增大R1的阻值时,
在如图所示的并联电路中,保持干路上的电流I不变,当增大R1的阻值时,