题目内容
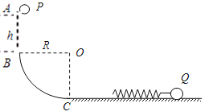
【题目】如图所示,光滑水平面上有三个滑块A、B、C,质量分别为![]() ,
,![]() ,
,![]() ,A、B用细绳连接,中间有一压缩的轻弹簧(与滑块不栓接). 开始时A、B以共同速度
,A、B用细绳连接,中间有一压缩的轻弹簧(与滑块不栓接). 开始时A、B以共同速度![]() 向右运动,C静止. 某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同.
向右运动,C静止. 某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同.

求:①B、C碰撞前的瞬间B的速度;
②整个运动过程中,弹簧释放的弹性势能与系统损失的机械能之比.
【答案】①![]() ,
,
②![]()
【解析】
试题分析:①A、B被弹开过程A、B系统动量守恒,以向右为正方向,
由动量守恒定律得:(mA+mB)v0=mAvA+mBvB,
对BC碰撞过程,由动量守恒定律得:(mC+mB)vC=mBvB,
且vC=vA,
解得:vC=vA=0.5v0,vB=2v0;
②从绳剪断到AB与弹簧分开的过程,对AB和弹簧满足能量守恒,则有:
![]() (m+2m)v02+EP=
(m+2m)v02+EP=![]() (2m)vA2+
(2m)vA2+![]() mvB2
mvB2
解得:EP=![]() mv02
mv02
根据全过程系统损失的机械能等于B、C碰撞前后损失的动能,则有:△E损=![]() mvB2
mvB2![]() (m+3m)vC2
(m+3m)vC2
解得:△E损=![]() mv02
mv02
则![]()

练习册系列答案
相关题目