题目内容
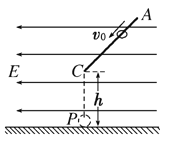
【题目】（18分）如图所示，在光滑的水平地面的左端连接一半径为R的
光滑圆形固定轨道，在水平面质量为M=3 m的小球Q连接着轻质弹簧，处于静止状态。现有一质量为m的小球P从B点正上方h=R高处由静止释放，求：
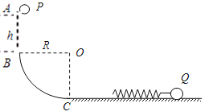
（1）小球P到达圆形轨道最低点C时的速度大小和对轨道的压力；
（2）在小球P压缩弹簧的过程中，弹簧具有的最大弹性势能；
（3）若球P从B上方高H处释放，恰好使P球经弹簧反弹后能够回到B点，则高度H的大小。
【答案】（1）vC=
（3分） 5mg（3分） （2）Epm=
（5分） （3）H=3R（7分）
【解析】（1）小球P从A运动到C过程，根据机械能守恒得
（2分）
又h=R，代入解得vC= （1分）
在最低点C处，根据牛顿第二定律有：
（2分）
解得轨道对小球P的支持力FN=5mg
根据牛顿第三定律知小球P对轨道的压力大小为5mg，方向竖直向下。（1分）
（2）弹簧被压缩过程中，当两球速度相等时，弹簧具有最大弹性势能，根据系统动量守恒有
mvC=(m+M)v （2分）
根据机械能守恒定律有
（2分）
联立解得EPm= （1分）
（3）球P从B上方高h处释放，到达水平面速度为v0，则有
Mg(H+R)＝
mv （1分）
弹簧被压缩后再次恢复到原长时，设小球P和Q的速度大小分别为v1和v2，根据动量守恒有
mv0=–mv1+Mv2 （1分）
根据机械能守恒有
（2分）
要使P球经弹簧反弹后恰好回到B点，则有
（2分）
联立解得H=3R（1分）
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
