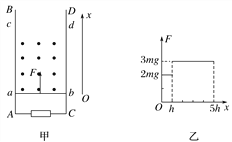
��Ŀ����
����Ŀ����ͼ��ʾ����ǿ�ų��ķ���ֱֽ�����һ�������Ӵų��߽�d�㴹ֱ�ڴų��������룬������dpa����MN�ϵ�a�㣬ͨ��pa����ʱΪt.����������P��ʱ����һ����ֹ�IJ���������ײ�����Ϊһ�����������մ���MN�ϡ�����������������������,�������˶��� ( )
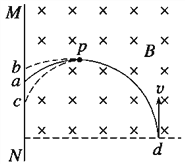
A. �켣Ϊpb,����Ļ��ʱ�佫С��t
B. �켣Ϊpc,����Ļ��ʱ�佫����t
C. �켣Ϊpa������Ļ��ʱ�佫����t
D. �켣Ϊpb,����Ļ��ʱ�佫����t
���𰸡�C
������������������ɶ����غ㶨�ɿɵó�������ײ����ܶ������䣬�������������������Ĺ�ϵ�ɵó��뾶����ʽ�����жϳ�����Ĺ켣�Ƿ�仯���������ڱ仯�ɵó�ʱ��ı仯��
�������ӺͲ������������������ض����غ㣬���ܶ������䣬�ܵ���Ҳ���ֲ��䣬��![]() ���ã�
���ã� ![]() ��P��q�����䣬��֪������ײǰ��Ĺ켣�뾶r���䣬�ʹ켣ӦΪpa��������
��P��q�����䣬��֪������ײǰ��Ĺ켣�뾶r���䣬�ʹ켣ӦΪpa��������![]() ��֪����m���������˶�����������������Ӧ�Ļ��߲��䣬Բ�ĽDz��䣬��pa���õ�ʱ�佫����t��C��ȷ��
��֪����m���������˶�����������������Ӧ�Ļ��߲��䣬Բ�ĽDz��䣬��pa���õ�ʱ�佫����t��C��ȷ��

��ϰ��ϵ�д�
 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
�����Ŀ