Question

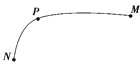
【题目】如图所示，长为l的轻质细线固定在O点，细线的下端系住质量为m、电荷量为＋q的小球，小球的最低点距离水平面的高度为h，在小球最低点与水平面之间高为h的空间内分布着场强为E的水平向右的匀强电场．固定点O的正下方l/2处有一小障碍物P，现将小球从细线处于水平状态由静止释放．

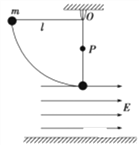
(1)细线在刚要接触障碍物P时，小球对细线的拉力为多少？

(2)若细线在刚好接触障碍物P时断开，小球运动到水平面时的动能为多大？

Answer 1

【答案】（2）3mg （2）mgh＋mgl＋＋2qE

【解析】(1)由机械能守恒定律得，

细线在刚要接触障碍物P时，设细线的拉力为，由牛顿第二定律得 ，

代入整理可以得到：

再根据牛顿第三定律可得，小球对细线的拉力，方向沿细绳竖直向上。

(2)细线断开后小球在竖直方向做自由落体运动，运动时间

小球在水平方向做匀加速运动，运动的距离

小球运动到水平面的过程由动能定理得

可得到： 。