题目内容
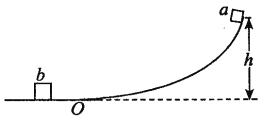
【题目】如图所示,A、B为固定在竖直平面内半径R=0.50m的四分之一圆弧轨道,过底端B点的切线水平,B点距水平地面的高度h=0.45m。一质量m=1.0kg的小滑块从圆弧轨道顶端A由静止释放,到达轨道底端B点的速度v=3.0m/s。取重力加速度g=10m/s2.求:

(1)小滑块落地点与B点的水平距离x。
(2)小滑块由A到B的过程中,克服摩擦力所做的功W;
(3)小滑块运动到圆弧轨道底端B点时对轨道的压力大小FN
【答案】(1)0.9m(2)0.5J;(3)28N
【解析】
(1)小滑块从B点出发做平抛运动,根据平抛运动的规律得
水平方向:x=vt
竖直方向:h=![]() gt2
gt2
解得:x=0.9m
(2)小滑块由A到B的过程中,根据动能定理得:mgR﹣W=![]() mv2
mv2
解得:W=mgR﹣![]() mv2=0.5J
mv2=0.5J
(3)小滑块在圆弧轨道底端B点受重力和支持力,
根据牛顿第二定律得:FN﹣mg=![]()
解得:FN=28N

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
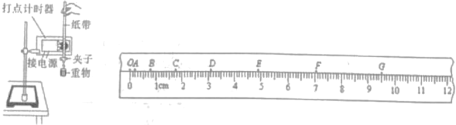
【题目】在“研究匀变速直线运动”的实验中,算出小车经过各计数点的瞬时速度如下,为了计算加速度,最合理的方法是
计数点序号 | 1 | 2 | 3 | 4 | 5 | 6 |
计数点对应的时刻(s) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
通过计数点的速度(cm/s) | 44.0 | 62.0 | 81.0 | 100.0 | 119.0 | 138.0 |
A.根据任意两计数点的速度用公式![]() 算出加速度
算出加速度
B.根据实验数据画出v-t图,量出其倾角,由公式![]() 求出加速度
求出加速度
C.根据实验数据画出v-t图,由图线上相距较远的两点所对应的速度、时间用公式![]() 算出加速度
算出加速度
D.依次算出通过连续两计数点间的加速度,算出平均值作为小车的加速度