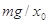题目内容
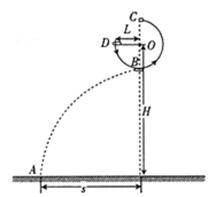
如图所示,倾角450高h的固定斜面。右边有一高3h/2的平台,平台顶部左边水平,上面有一质量为M的静止小球B,右边有一半径为h的1/4圆弧。质量为m的小球A从斜面底端以某一初速度沿斜面上滑,从斜面最高点飞出后恰好沿水平方向滑上平台,与B发生弹性碰撞,碰后B从圆弧上的某点离开圆弧。所有接触面均光滑,A、B均可视为质点,重力加速度为g。
(1)求斜面与平台间的水平距离S和A的初速度v0;
(2)若M=2m,求碰后B的速度;
(3)若B的质量M可以从小到大取不同值,碰后B从圆弧上不同位置脱离圆弧,该位置与圆心的连线和竖直方向的夹角为α。求cosα的取值范围。

(1)求斜面与平台间的水平距离S和A的初速度v0;
(2)若M=2m,求碰后B的速度;
(3)若B的质量M可以从小到大取不同值,碰后B从圆弧上不同位置脱离圆弧,该位置与圆心的连线和竖直方向的夹角为α。求cosα的取值范围。
(1)h  (2)
(2) (3)
(3)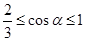
 (2)
(2) (3)
(3)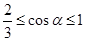
试题分析:(1)设小球A飞上平台的速度为
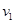 ,小球由斜面顶端飞上平台,可看成以速度v1反向平抛运动,由平抛运动规律得:
,小球由斜面顶端飞上平台,可看成以速度v1反向平抛运动,由平抛运动规律得: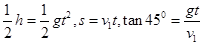
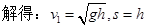 (4分)
(4分)由机械能守恒定律得:
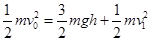
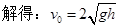 (3分)
(3分)(2)设碰后A、B的速度分别为
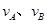 ,由动量、能量守恒得
,由动量、能量守恒得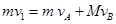
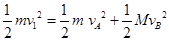
 (6分)
(6分)(3)由(2)可知,当M<<m时
 从顶端飞离则
从顶端飞离则 (2分)
(2分)当M>>m时,
 =0,设B球与圆弧面在C处分离,则:
=0,设B球与圆弧面在C处分离,则:
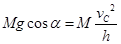
 (4分)
(4分)故
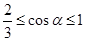 (1分)
(1分)
练习册系列答案
相关题目



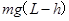
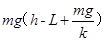
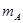 、
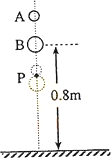
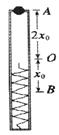
、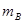 的两个小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在B球的正上方。 先将B球释放,经过一段时间后再将A球释放。 当A球下落t=0.3s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰为零。已知
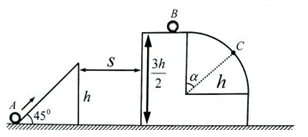
的两个小球A、B静止在地面上方,B球距地面的高度h=0.8m,A球在B球的正上方。 先将B球释放,经过一段时间后再将A球释放。 当A球下落t=0.3s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰为零。已知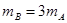 ,重力加速度大小为
,重力加速度大小为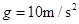 ,忽略空气阻力及碰撞中的动能损失。
,忽略空气阻力及碰撞中的动能损失。