题目内容
1. 一小木块放在圆盘上,小木块m=1kg,距转轴r=4cm,圆盘转ω=10rad/s,小木块与圆盘动摩擦因数μ=0.3,设小木块受最大静摩擦力等于滑动摩擦力,小木块在该处能否处于相对静止状态?在该处处于静止的最大ω是多大?(g=10m/s2)
一小木块放在圆盘上,小木块m=1kg,距转轴r=4cm,圆盘转ω=10rad/s,小木块与圆盘动摩擦因数μ=0.3,设小木块受最大静摩擦力等于滑动摩擦力,小木块在该处能否处于相对静止状态?在该处处于静止的最大ω是多大?(g=10m/s2)
分析 根据线速度与角速度的关系,求出线速度的大小,根据静摩擦力提供向心力求出摩擦力的大小,比较两个力的大小即可判断能否静止,若不能,当静摩擦力达到最大静摩擦力时,角速度最大,根据向心力公式即可求解.
解答 解:小木块做圆周运动,静摩擦力提供向心力,
小木块所需向心力${F}_{n}=m{ω}^{2}r=1×100×0.04=4N$
小木块的最大静摩擦力Ff=μmg=0.3×110=3N
因为Ff<Fn,故不能处于相对静止状态;
当最大静摩擦力提供向心力时ω最大,
令${F}_{f}=m{ω}^{2}r$,解得${ω}_{m}=5\sqrt{3}rad/s$,
答:小木块在该处不能处于相对静止状态,在该处处于静止的最大ω是$5\sqrt{3}rad/s$.
点评 解决本题的关键知道圆周运动向心力的来源,结合牛顿第二定律进行求解,以及知道向心力与角速度的大小关系.

练习册系列答案
相关题目
11.某放射性元素的原子核发生两次α衰变和六次β衰变,关于它的原子核的变化,下列说法中正确的是( )
| A. | 核子数减小8 | B. | 质子数减小2 | C. | 质子数增加2 | D. | 中子数减小10 |
16.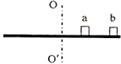 如图.两个小木块a(质量为2m)和b(质量为m)均可视为质点,放在水平圆盘上,a与转轴00'的距离为l,b与转轴的距离为2l.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用表示圆盘转动的角速度,下列说法错误的是( )
如图.两个小木块a(质量为2m)和b(质量为m)均可视为质点,放在水平圆盘上,a与转轴00'的距离为l,b与转轴的距离为2l.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用表示圆盘转动的角速度,下列说法错误的是( )
 如图.两个小木块a(质量为2m)和b(质量为m)均可视为质点,放在水平圆盘上,a与转轴00'的距离为l,b与转轴的距离为2l.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用表示圆盘转动的角速度,下列说法错误的是( )
如图.两个小木块a(质量为2m)和b(质量为m)均可视为质点,放在水平圆盘上,a与转轴00'的距离为l,b与转轴的距离为2l.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用表示圆盘转动的角速度,下列说法错误的是( )| A. | b一定比a先开始滑动 | |
| B. | 当ω<$\sqrt{\frac{kg}{2l}}$,a、b所受的摩擦力大小始终相等 | |
| C. | ω=$\sqrt{\frac{kg}{2l}}$是b开始滑动的临界角速度 | |
| D. | 当ω=$\sqrt{\frac{2kg}{2l}}$时,a所受摩擦力的大小为$\frac{2kmg}{3}$ |
6. 伽利略的斜面实验反映了一个重要事实:如果空气阻力和摩擦力小到可以忽略不计,小球一但沿斜面A滚落,必将准确地终止于斜面B上同它开始点相同高度处,绝不会更高一点或更低一点,这说明,小球在运动过程中有一个“东西”是不变的,这个“东西”是( )
伽利略的斜面实验反映了一个重要事实:如果空气阻力和摩擦力小到可以忽略不计,小球一但沿斜面A滚落,必将准确地终止于斜面B上同它开始点相同高度处,绝不会更高一点或更低一点,这说明,小球在运动过程中有一个“东西”是不变的,这个“东西”是( )
 伽利略的斜面实验反映了一个重要事实:如果空气阻力和摩擦力小到可以忽略不计,小球一但沿斜面A滚落,必将准确地终止于斜面B上同它开始点相同高度处,绝不会更高一点或更低一点,这说明,小球在运动过程中有一个“东西”是不变的,这个“东西”是( )
伽利略的斜面实验反映了一个重要事实:如果空气阻力和摩擦力小到可以忽略不计,小球一但沿斜面A滚落,必将准确地终止于斜面B上同它开始点相同高度处,绝不会更高一点或更低一点,这说明,小球在运动过程中有一个“东西”是不变的,这个“东西”是( )| A. | 弹力 | B. | 速度 | C. | 加速度 | D. | 能量 |
13. A、B两颗地球卫星在同一轨道中同向运行,如图所示,若要使B卫星追上A卫星,下列方法可行的有( )
A、B两颗地球卫星在同一轨道中同向运行,如图所示,若要使B卫星追上A卫星,下列方法可行的有( )
 A、B两颗地球卫星在同一轨道中同向运行,如图所示,若要使B卫星追上A卫星,下列方法可行的有( )
A、B两颗地球卫星在同一轨道中同向运行,如图所示,若要使B卫星追上A卫星,下列方法可行的有( )| A. | B卫星减速 | B. | B卫星加速 | ||
| C. | B卫星先减速,再加速 | D. | B卫星先加速,再减速 |
16.甲、乙两个物体在同一直线上运动,它们的速度-时间图象如图所示,在t0时刻( )
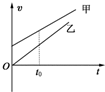

| A. | 甲的加速度比乙的加速度大 | B. | 甲的加速度等于乙的加速度 | ||
| C. | 甲的速度比乙的速度大 | D. | 甲的速度比乙的速度小 |
 在四川省汶川抗震救灾中,解放军用直升机给灾民投放物品.如果所投物品的质量为m,投放物品的水平初速度为v0,物品经时间t落地,不计空气阻力.试求以下问题:
在四川省汶川抗震救灾中,解放军用直升机给灾民投放物品.如果所投物品的质量为m,投放物品的水平初速度为v0,物品经时间t落地,不计空气阻力.试求以下问题: 如图所示,将单匝正方形线圈ABCD的一半放入匀强磁场中,磁场的磁感应强度B=1T,让它以边界OO′为轴以角速度ω=100rad/s匀速转动,在AB、CD边的中点用电枢将电流输送给小灯泡,线圈边长L=0.2m,总电阻r=4Ω,灯泡电阻R=2Ω,不计P、Q接触电阻及导线电阻,求:
如图所示,将单匝正方形线圈ABCD的一半放入匀强磁场中,磁场的磁感应强度B=1T,让它以边界OO′为轴以角速度ω=100rad/s匀速转动,在AB、CD边的中点用电枢将电流输送给小灯泡,线圈边长L=0.2m,总电阻r=4Ω,灯泡电阻R=2Ω,不计P、Q接触电阻及导线电阻,求: