题目内容
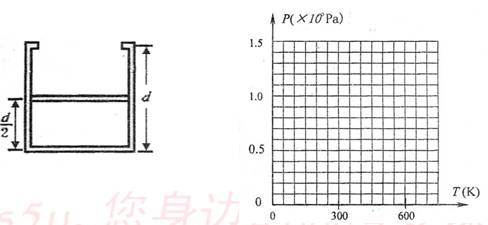
如图所示，气缸呈圆柱形，上部有挡板，内部高度为d．筒内有一个很薄的质量不计的活塞封闭一定量的气体，开始时活塞处于离底部d/2的高度，外界大气压强为1×l05帕，温度为27℃，现对气体加热．求：（1）气体温度达到127℃，活塞离底部的高度．
（2）气体温度达到387℃时，活塞离底部的高度和气体的压强．
【答案】分析：（1）根据盖吕萨克定律求出活塞刚好到达顶部时气体的临界温度．
对气体缓缓加热时，气体发生等压变化，由盖吕萨克定律求解气体温度升高到127℃时，活塞离底部的高度．
（2）若温度387℃高于临界温度时，气体发生等容变化，根据查理这定律求解缸内气体的压强．
解答：解：（1）以封闭气体为研究对象：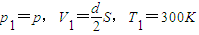
；
设温度升高到T时，活塞刚好到达汽缸口．此时有：p2=p，V2=dS，T2；
根据盖?吕萨克定律：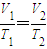
，得T2=600K．
由于T3=400K＜T2，故有p3=p，V3=l3S，T3=400K；
由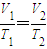
，得
．
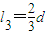（2）T4=660K＞T2，封闭气体先做等压变化，活塞到达汽缸口之后做等容变化．
所以：l4=d
此时有：p4，V4=dS，T4=600K；
由理想气体状态方程：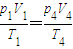
，
解得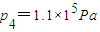
答：（1）气体温度达到127℃，活塞离底部的高度为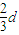
．
（2）气体温度达到387℃时，活塞离底部的高度为d，气体的压强为1.1×105Pa．
点评：本题关键要确定气体状态变化过程，再选择合适的规律求解，同时，要挖掘隐含的临界状态进行判断．
对气体缓缓加热时，气体发生等压变化，由盖吕萨克定律求解气体温度升高到127℃时，活塞离底部的高度．
（2）若温度387℃高于临界温度时，气体发生等容变化，根据查理这定律求解缸内气体的压强．
解答：解：（1）以封闭气体为研究对象：
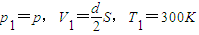；设温度升高到T时，活塞刚好到达汽缸口．此时有：p2=p，V2=dS，T2；
根据盖?吕萨克定律：
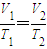，得T2=600K．由于T3=400K＜T2，故有p3=p，V3=l3S，T3=400K；
由
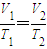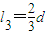，得．（2）T4=660K＞T2，封闭气体先做等压变化，活塞到达汽缸口之后做等容变化．
所以：l4=d
此时有：p4，V4=dS，T4=600K；
由理想气体状态方程：
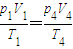，解得
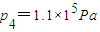
答：（1）气体温度达到127℃，活塞离底部的高度为
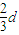．（2）气体温度达到387℃时，活塞离底部的高度为d，气体的压强为1.1×105Pa．
点评：本题关键要确定气体状态变化过程，再选择合适的规律求解，同时，要挖掘隐含的临界状态进行判断．
练习册系列答案
相关题目
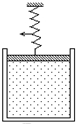如图所示，在一个圆柱形导热的气缸中，用活塞封闭了一部分空气，活塞与气缸壁间是密封而光滑的，一弹簧秤挂在活塞上，将整个气缸悬吊在天花板上．当外界气温升高（大气压不变）时（ ）
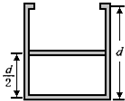（2005?上海模拟）如图所示，气缸呈圆柱形，上部有挡板，内部高度为d．筒内有一个很薄的质量不计的活塞封闭一定量的气体，开始时活塞处于离底部d/2的高度，外界大气压强为1×l05帕，温度为27℃，现对气体加热．求：
