题目内容
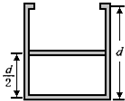（2005?上海模拟）如图所示，气缸呈圆柱形，上部有挡板，内部高度为d．筒内有一个很薄的质量不计的活塞封闭一定量的气体，开始时活塞处于离底部d/2的高度，外界大气压强为1×l05帕，温度为27℃，现对气体加热．求：（1）气体温度达到127℃，活塞离底部的高度．
（2）气体温度达到387℃时，活塞离底部的高度和气体的压强．
分析：（1）根据盖吕萨克定律求出活塞刚好到达顶部时气体的临界温度．
对气体缓缓加热时，气体发生等压变化，由盖吕萨克定律求解气体温度升高到127℃时，活塞离底部的高度．
（2）若温度387℃高于临界温度时，气体发生等容变化，根据查理这定律求解缸内气体的压强．
对气体缓缓加热时，气体发生等压变化，由盖吕萨克定律求解气体温度升高到127℃时，活塞离底部的高度．
（2）若温度387℃高于临界温度时，气体发生等容变化，根据查理这定律求解缸内气体的压强．
解答：解：（1）以封闭气体为研究对象：p1=p0，V1=
S，T1=300K；
设温度升高到T0时，活塞刚好到达汽缸口．此时有：p2=p0，V2=dS，T2；
根据盖?吕萨克定律：
=
，得T2=600K．
由于T3=400K＜T2，故有p3=p0，V3=l3S，T3=400K；
由
=
，得l3=
d．
（2）T4=660K＞T2，封闭气体先做等压变化，活塞到达汽缸口之后做等容变化．
所以：l4=d
此时有：p4，V4=dS，T4=600K；
由理想气体状态方程：
=
，
解得 p4=1.1×105Pa
答：（1）气体温度达到127℃，活塞离底部的高度为
d．
（2）气体温度达到387℃时，活塞离底部的高度为d，气体的压强为1.1×105Pa．
| d |
| 2 |
设温度升高到T0时，活塞刚好到达汽缸口．此时有：p2=p0，V2=dS，T2；
根据盖?吕萨克定律：
| V1 |
| T1 |
| V2 |
| T2 |
由于T3=400K＜T2，故有p3=p0，V3=l3S，T3=400K；
由
| V1 |
| T1 |
| V2 |
| T2 |
| 2 |
| 3 |
（2）T4=660K＞T2，封闭气体先做等压变化，活塞到达汽缸口之后做等容变化．
所以：l4=d
此时有：p4，V4=dS，T4=600K；
由理想气体状态方程：
| p1V1 |
| T1 |
| p4V4 |
| T4 |
解得 p4=1.1×105Pa
答：（1）气体温度达到127℃，活塞离底部的高度为
| 2 |
| 3 |
（2）气体温度达到387℃时，活塞离底部的高度为d，气体的压强为1.1×105Pa．
点评：本题关键要确定气体状态变化过程，再选择合适的规律求解，同时，要挖掘隐含的临界状态进行判断．
练习册系列答案
相关题目
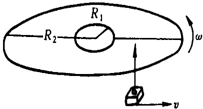（2005?上海模拟）一光盘（CD）音轨区域的内半径R1=25mm，外半径R2=58mm，径向音轨密度n=625条/mm．在CD唱机中，光盘每转一圈，激光头沿径向向外移动一条音轨，激光头对光盘以恒定的线速度运动．若开始放音时，光盘的角速度为50rad/s，则全部放完时的角速度是
（2005?上海模拟）用如图所示的传统打气筒给容器打气，设打气筒的容积为V0，底部有一阀门K可自动开启并不漏气，活塞A上提时外界大气可从其四周进入打气筒，活塞下移时可把打气筒内气体推入B中．若B的容积为4V0，A、B内气体初始压强等于大气压P0，为使B中气体压强达到10P0，则需打气
（2005?上海模拟）如图所示，硬杆一端铰链固定在墙上的B点，另一端装有滑轮，重物用绳拴住通过滑轮固定于墙上的A点，若杆、滑轮及绳的质量和摩擦均不计，将绳的固定端从A点稍向下移，再使之平衡时，则（ ）