题目内容
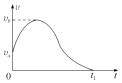
【题目】甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动．质点甲做初速度为零，加速度大小为a1的匀加速直线运动．质点乙做初速度为v0 ， 加速度大小为a2的匀减速直线运动至速度减为零保持静止．甲、乙两质点在运动过程中的位置x﹣速度v图象如图所示，虚线与对应的坐标轴垂直．
（1）在x﹣v图象中，图线a表示质点（填“甲”或“乙”）的运动，质点乙的初速度v0=；
（2）求质点甲、乙的加速度大小a1、a2 ．
【答案】
（1）甲,6m/s
（2）解：设质点乙、甲先后通过x=6m处时的速度均为v，对质点甲：v2=2a1x①
对质点乙： 
②
联立①②解得： 
③
当质点甲的速度v1=8m/s、质点乙的速度v2=2m/s时，两质点通过相同的位移均为x'．
对质点甲： 
④
对质点乙： 
⑤
联立④⑤解得：a1=2a2⑥
联立③⑥解得： 
， 
所以质点甲、乙的加速度大小a1、a2分别为2m/s2和1m/s2．
【解析】解：（1）根据图象可知，a图象的速度随位移增大而增大，b图象的速度随位移增大而减小，所以图象a表示质点甲的运动，
当x=0时，乙的速度为6m/s，即质点乙的初速度v0=6m/s．
所以答案是：甲；6m/s；
【考点精析】本题主要考查了匀变速直线运动的速度、位移、时间的关系和S-t图象的相关知识点，需要掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值；s-t图像：①图像上一点切线的斜率表示该时刻所对应速度；②图像是直线表示物体做匀速直线运动，图像是曲线则表示物体做变速运动；③图像与横轴交叉，表示物体从参考点的一边运动到另一边才能正确解答此题．
