Question

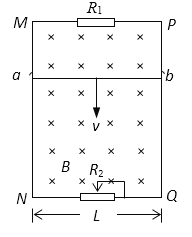
【题目】图中MN和PQ为竖直方向的两平行长直金属导轨，间距L为0.40m，电阻不计。导轨所在平面与磁感应强度B为0.50T的匀强磁场垂直。质量为m =6.0×10-3kg、电阻r=1.0Ω的金属杆ab始终垂直于导轨，并与其保持光滑接触。导轨两端分别接有滑动变阻器和定值电阻=3.0Ω的。当杆ab达到稳定状态时以速率v匀速下滑，整个电路消耗的电功率P为0.27W，重力加速度取10m/s2，试求：

（1）速率v；

（2）滑动变阻器接入电路部分的阻值；

（3）若杆ab由静止开始下滑，达到稳定速率v所需的时间t为0.5s，求这段时间通过ab棒的电荷量q。

Answer 1

【答案】（1）V=4.5m/s；（2）=6.0Ω；（3）q=

【解析】

设杆稳定时，流过棒的电流为I，分析可知稳定时棒将做匀速直线运动，棒重力势能的减少量完全转化为焦耳热。

（1）由能量守恒则有

①

得v=4.5m/s ②

（2）感应电动势为E=BLv ③

④

⑤

⑥

由①②③④⑤⑥带入数据得=6.0Ω

（3）对ab棒应用动量定理

⑦

⑧

由②⑦⑧带入数据得q=