Question

【题目】如图所示，在方向竖直向上、大小为E=1×106V/m的匀强电场中，固定一个穿有A、B两个小球（均视为质点）的光滑绝缘圆环，圆环在竖直平面内，圆心为O、半径为R=0.2m。A、B用一根绝缘轻杆相连，A带的电荷量为q=+7×10-7C，B不带电，质量分别为mA=0.01kg、mB=0.08kg。将两小球从圆环上的图示位置（A与圆心O等高，B在圆心O的正下方）由静止释放，两小球开始沿逆时针方向转动。取g=10m/s2。

（1）通过计算判断，小球A能否到达圆环的最高点C。

（2）求小球A的最大速度值。（可保留根号）

（3）求小球A从图示位置逆时针转动的过程中，其电势能变化的最大值。

Answer 1

【答案】（1）A不能到达圆环最高点（2）（3）

【解析】试题分析：设A、B在转动过程中，轻杆对A、B做的功分别为、,对A、B分列动能定理，求出动能之和，结果表明，A在圆环最高点时，系统动能为负值。故A不能到达圆环最高点；设B转过α角时，A、B的速度大小分别为vA、vB，因A、B做圆周运动的半径和角速度均相同，故vA=vB，对A、B分列动能定理，根据数学知识求出最大速度；A、B从图示位置逆时针转动过程中，当两球速度为0时，电场力做功最多，电势能减少最多，在结合数学知识即可解题。

（1）设A、B在转动过程中，轻杆对A、B做的功分别为、，则

设A、B到达圆环最高点的动能分别为、

对A由动能定理：

对B由动能定理：

联立解得：

上式表明，A在圆环最高点时，系统动能为负值。故A不能到达圆环最高点。

（2）设B转过α角时，A、B的速度大小分别为vA、vB，因A、B做圆周运动的半径和角速度均相同，故vA=vB

对A由动能定理：

对B由动能定理：

联立解得：

解得当时，A、B的最大速度均为

（3）A、B从图示位置逆时针转动过程中，当两球速度为0时，电场力做功最多，电势能减少 最多，故得：

解得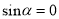： （舍去）

故A的电势能减少量：

代入数值得：