题目内容
2.一辆质量m=2t的轿车,驶过半径R=90m的一段凸形桥面,g取10m/s2,求:(1)轿车以10m/s的速度通过桥面最高点时,对桥面的压力是多大?
(2)在最高点对桥面的压力等于轿车重力的一半时,车的速度大小是多少?
分析 (1)轿车在凹形桥和凸形桥的最低点和最高点,靠重力和支持力的合力提供向心力,根据牛顿第二定律求出桥面对轿车的支持力,从而得出轿车对桥面的压力.
(2)在最高点对桥面的压力等于轿车重力的一半时,靠重力和支持力的合力提供向心力,根据牛顿第二定律求出汽车的速度.
解答  解:(1)轿车通过凸形桥面最高点时,受力分析如图所示:
解:(1)轿车通过凸形桥面最高点时,受力分析如图所示:
则合力为:F=mg-FN,
由向心力公式得:mg-FN=$m\frac{{v}^{2}}{R}$
故桥面的支持力大小为:FN=mg-$m\frac{{v}^{2}}{R}$=(2 000×10-2 000×)N=1.78×104 N
根据牛顿第三定律,轿车在桥的顶点时对桥面压力的大小为1.78×104 N.
(2)对桥面的压力等于轿车重力的一半时,则有:
F′=mg-$m\frac{{v′}^{2}}{R}$
而F′=0.5mg,
所以此时轿车的速度大小为:v$′=\sqrt{0.5Rg}=15\sqrt{2}m/s$
答:(1)轿车以10m/s的速度通过桥面最高点时,对桥面的压力是1.78×104 N;
(2)在最高点对桥面的压力等于轿车重力的一半时,车的速度大小是$15\sqrt{2}m/s$.
点评 解决本题的关键搞清向心力的来源,根据牛顿第二定律进行求解,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.关于“探究功与速度变化的关系”的实验中,下面的说法中有一项不正确,它是( )
| A. | 本实验设法让橡皮筋对小车做的功分别为W、2W、3W、….所采用的方法是选用同样的橡皮筋,并在每次实验中使橡皮筋拉伸的长度保持一致.当用l条橡皮筋进行是实验时,橡皮筋对小车做的功为W,用2条、3条、…橡皮筋并在一起进行第2次、第3次…实验时,橡皮筋对小车做的功分别是2W、3W、… | |
| B. | 小车运动中会受到阻力,补偿的方法,可以使木板适当倾斜 | |
| C. | 某同学在一次实验中,得到一条记录纸带.纸带上打出的点,两端密、中间疏.出现这种情况的原因,可能是没有使木板倾斜或倾角太小 | |
| D. | 根据记录纸带上打出的点,求小车获得的速度的方法,是以纸带上第一点到最后一点的距离来进行计算 |
7.探月工程三期飞行试验器于2014年10月24日2时在中国西昌卫星发射中心发射升空,飞行试验器飞抵距月球6万千米附近进入月球引力影响区,开始在月球近旁转向飞行,最终进入距月球表面h=200km的圆形工作轨道.设月球半径为R,月球表面的重力加速度为g,万有引力常量为G,则下列选项错误的是( )
| A. | 飞行试验器在工作轨道上的绕行速度为R$\sqrt{\frac{g}{R+h}}$ | |
| B. | 飞行试验器工作轨道处的重力加速度为($\frac{R}{R+h}$)2g | |
| C. | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| D. | 月球的平均密度为$\frac{3g}{4πGR}$ |
12.下面的实例中,机械能守恒的是( )
| A. | 物体在粗糙的地面上滑行 | |
| B. | 拉着物体沿光滑的斜面匀速上升 | |
| C. | 跳伞运动员张开伞后,在空中匀速下降 | |
| D. | 作自由落体运动的物体 |
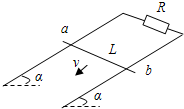 如图所示,宽度为L=1m的导轨与水平面成37°角倾斜放置,上端串接一个阻值为1Ω的定值电阻R,导体棒ab的电阻为r=0.5Ω,质量为0.1kg.其余电阻不计.空间有垂直导轨平面的匀强磁场,磁感应强度B=0.4T.已知,导体棒从静止开始下滑,能达到的最大速度为5m/s,(sin37°=0.6,Cos37°=0.8)求
如图所示,宽度为L=1m的导轨与水平面成37°角倾斜放置,上端串接一个阻值为1Ω的定值电阻R,导体棒ab的电阻为r=0.5Ω,质量为0.1kg.其余电阻不计.空间有垂直导轨平面的匀强磁场,磁感应强度B=0.4T.已知,导体棒从静止开始下滑,能达到的最大速度为5m/s,(sin37°=0.6,Cos37°=0.8)求 在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B按如图乙所示的规律变化.求:
在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B按如图乙所示的规律变化.求: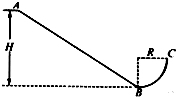 如图所示,总质量为m=60kg,可视为质点的滑雪运动员(包括装备)从高为H=30m的斜面AB的顶端A点由静止开始沿斜面下滑,在B点进入四分之一圆弧轨道BC,圆弧半径R=5m,运动员在C点沿竖直方向冲出轨道,经过时间4s又从C点落回轨道.若运动员从C点离开轨道后受到的空气阻力不计,g取10m/s2.求:
如图所示,总质量为m=60kg,可视为质点的滑雪运动员(包括装备)从高为H=30m的斜面AB的顶端A点由静止开始沿斜面下滑,在B点进入四分之一圆弧轨道BC,圆弧半径R=5m,运动员在C点沿竖直方向冲出轨道,经过时间4s又从C点落回轨道.若运动员从C点离开轨道后受到的空气阻力不计,g取10m/s2.求: