题目内容
10.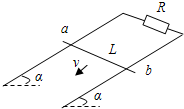 如图所示,宽度为L=1m的导轨与水平面成37°角倾斜放置,上端串接一个阻值为1Ω的定值电阻R,导体棒ab的电阻为r=0.5Ω,质量为0.1kg.其余电阻不计.空间有垂直导轨平面的匀强磁场,磁感应强度B=0.4T.已知,导体棒从静止开始下滑,能达到的最大速度为5m/s,(sin37°=0.6,Cos37°=0.8)求
如图所示,宽度为L=1m的导轨与水平面成37°角倾斜放置,上端串接一个阻值为1Ω的定值电阻R,导体棒ab的电阻为r=0.5Ω,质量为0.1kg.其余电阻不计.空间有垂直导轨平面的匀强磁场,磁感应强度B=0.4T.已知,导体棒从静止开始下滑,能达到的最大速度为5m/s,(sin37°=0.6,Cos37°=0.8)求(1)达到稳定速度时,电阻R上消耗的热功率为多大?
(2)ab与导轨之间的动摩擦因素为多大?
分析 导体棒匀速运动时达到稳定状态,根据平衡条件可求出摩擦力大小,再求动摩擦因数.
再由功能关系求出回路总的电功率,由串联电路的关系求解R上消耗的热功率.
解答 解:(1)设导体棒所受的摩擦力大小为f.
根据平衡条件得:mgsin37°=f+BIL
又 I=$\frac{BLv}{R+r}$
解得 f=mgsin37°-$\frac{{B}^{2}{L}^{2}v}{R+r}$=0.1×10×0.6-$\frac{0.{4}^{2}×{1}^{2}×5}{1+0.5}$=$\frac{1}{15}$N
回路总的电功率为 P=(mgsin37°-f)•v=(0.1×10×0.6-$\frac{1}{15}$)×5W=$\frac{8}{3}$W
故电阻R上消耗的热功率为 PR=$\frac{R}{R+r}$P=$\frac{1}{1.5}$×$\frac{8}{3}$W=$\frac{16}{9}$W
(2)ab与导轨之间的动摩擦因素为 μ=$\frac{f}{N}$
而N=mgcos37°
解得 μ=$\frac{1}{12}$.
答:
(1)达到稳定速度时,电阻R上消耗的热功率为$\frac{16}{9}$W.
(2)ab与导轨之间的动摩擦因素为$\frac{1}{12}$.
点评 电磁感应中导体切割类型,关键要应明确导体棒达到稳定时做匀速运动,受力平衡,根据平衡条件和功能关系分析和处理这类问题.

练习册系列答案
相关题目
4.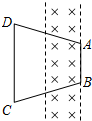 如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合,AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.先让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )
如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合,AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.先让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )
 如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合,AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.先让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )
如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合,AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.先让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )| A. | 线圈中感应电流沿逆时针方向 | B. | 线圈中感应电动势大小为BLv | ||
| C. | 通过线圈截面的电量为$\frac{B{L}^{2}}{R}$ | D. | 线圈克服安培力做的功为$\frac{{B}^{2}{L}^{2}v}{4R}$ |
1.一定质量理想气体处于平衡状态Ⅰ,现使其温度降低而压强升高,达到平衡状态Ⅱ,则以下判断正确的是( )
| A. | 状态Ⅰ时气体的密度比状态Ⅱ时的大 | |
| B. | 状态Ⅰ时各个分子的动能比状态Ⅱ时的大 | |
| C. | 状态Ⅰ时分子的平均距离比状态Ⅱ时的大 | |
| D. | 状态Ⅰ时单个分子对器壁平均撞击力比状态Ⅱ时小 |
5.下列说法中正确的是( )
| A. | 物体只要存在加速度,物体的速度就增大 | |
| B. | 只要物体的加速度为正,物体的速度一定增大 | |
| C. | 物体的加速度增大,物体的速度一定增大 | |
| D. | 加速度在减小,物体的速度可能增大 |
15.西昌卫星发射中心的火箭发射架上,有一待发射的卫星,它随地球自转的线速度为v1、加速度为a1;发射升空后在近地轨道上做匀速圆周运动,线速度为v2、加速度为a2;实施变轨后,使其在同步卫星轨道上做匀速圆周运动,运动的线速度为v3、加速度为a3.则v1、v2、v3的大小关系和a1、a2、a3的大小关系是( )
| A. | v3>v2>v1 ,a2>a3>a1 | B. | v2>v3=v1 ,a2=a1>a3 | ||
| C. | v2>v3>v1 ,a2>a3>a1 | D. | v2>v3>v1 ,a3>a2>a1 |
19.关于物体做曲线运动的条件,以下说法中正确的是( )
| A. | 物体在恒力作用下,不可能做曲线运动 | |
| B. | 物体在受到与速度不在同一直线上力的作用下,一定做曲线运动 | |
| C. | 物体在变力作用下,一定做曲线运动 | |
| D. | 物体在变力作用下,不可能做直线运动 |
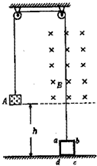 如图所示,在距离水平地面h=0.8m的虚线的上方有一个方向垂直于纸面水平向内的匀强磁场.正方形线框abcd的边长l=0.2m,质量m=0.1kg,电阻R=0.08Ω.一条不可伸长的轻绳绕过轻滑轮,一端连线框,另一端连一质量M=0.2kg的物体A.开始时线框的cd边在地面上,各段绳都处于伸直状态,从如图所示的位置由静止释放物体A,一段时间后线框进入磁场运动,已知线框的ab边刚进入磁场时线框恰好做匀速运动.当线框的cd边进入磁场时物体A恰好落地,同时将轻绳剪断,线框继续上升一段时间后开始下落,最后落至地面.整个过程线框没有转动,线框平面始终处于纸面内,g取10m/s2.求:
如图所示,在距离水平地面h=0.8m的虚线的上方有一个方向垂直于纸面水平向内的匀强磁场.正方形线框abcd的边长l=0.2m,质量m=0.1kg,电阻R=0.08Ω.一条不可伸长的轻绳绕过轻滑轮,一端连线框,另一端连一质量M=0.2kg的物体A.开始时线框的cd边在地面上,各段绳都处于伸直状态,从如图所示的位置由静止释放物体A,一段时间后线框进入磁场运动,已知线框的ab边刚进入磁场时线框恰好做匀速运动.当线框的cd边进入磁场时物体A恰好落地,同时将轻绳剪断,线框继续上升一段时间后开始下落,最后落至地面.整个过程线框没有转动,线框平面始终处于纸面内,g取10m/s2.求: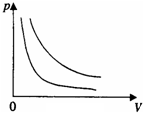 某同学利用DIS实验系统,用同一个注射器在实验室前后做了两次验证波意耳定律的实验,操作完全正确.
某同学利用DIS实验系统,用同一个注射器在实验室前后做了两次验证波意耳定律的实验,操作完全正确.