题目内容

8．质量为m的运动员从下蹲状态竖直向上起跳，经过时间t，身体伸直并刚好离开地面，离开地面时速度为v在时间t内（　　）
A．地面对他的平均作用力为mgB．地面对他的平均作用力为$\frac{mv}{t}$
C．地面对他的平均作用力为m（$\frac{v}{t}$-g）D．地面对他的平均作用力为m（g+$\frac{v}{t}$）

分析 已知初末速度，则由动量定理可求得地面对人的平均作用力．

解答 解：人的速度原来为零，起跳后变化v，则由动量定理可得：
$\overline{F}t$-mgt=△mv=mv
所以：$\overline{F}$=m（g+$\frac{v}{t}$）；故D正确，ABC错误；
故选：D

点评 在应用动量定理时一定要注意冲量应是所有力的冲量，不要把重力漏掉．

练习册系列答案
相关题目
12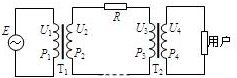．如图所示，有一台交流发电机E，通过理想升压变压器T1和理想降压变压器T2向远处用户供电，输电线的总电阻为R．T1的输入电压和输入功率分别为U1和P1，它的输出电压和输出功率分别为U2和P2；T2的输入电压和输入功率分别为U3和P3，它的输出电压和输出功率分别为U4和P4．设T1的输入电压U1一定，当用户消耗的电功率变大时，有（　　）
A．U2不变，U3变小B．U2减小，U4变大C．P2变大，P3变大D．P1不变，P2变小
13．如图所示，某回旋加速器的两个半圆金属盒处于与盒面垂直的匀强磁场中，两金属盒间存在交变电场，用其加速质子．已知金属盒的半径R为16cm，磁场的磁感应强度B为1.3T，质子穿过金属盒间的缝隙时加速电压U为10kV，取质子的质量m为1.6×10-27 kg，电荷量q为1.6×10-19C．求
（1）交变电场的频率f；
（2）质子出射时的动能Ek；
（3）质子在回旋加速器中运动的圈数n．
16．有三个共点力F1、F2、F3作用于某一点，其合力为零．已知F3=5N，现保持其余两力大小和方向不变，只将F3的方向沿顺时针方向绕作用点转动60°，则这三个力的合力大小变为（　　）
A．5$\sqrt{3}$NB．5NC．10ND．仍为零
3．在空中下落的雨滴，受到的空气阻力随雨滴下落的速度增大而逐渐增大，在阻力等于重力后，雨滴匀速下落，则雨滴在此后的下落过程中，重力的瞬时功率P1和阻力的瞬时功率P2的大小关系是（　　）
A．P1＞P2B．P1＜P2
C．P1=P2D．条件不足，无法判断
13．粗糙水平面上，用水平绳子系一小球作半径为R的匀速圆周运动，小球质量为m，与桌面间的摩擦系数为μ，绳子的拉力为F，则小球经过$\frac{1}{2}$圆周的时间内（　　）
A．绳子的拉力对球不做功B．绳子的拉力对球做功πRF
C．重力和支持力不做功D．摩擦力对物体做功-μmgRπ
20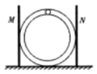．如图所示，内壁光滑的圆管形轨道竖直放置在光滑水平地面上，且恰好处在两固定光滑挡板M、N之间，圆轨道半径为R，其质量为2m，一质量为m的小球能在管内运动，小球可视为质点，管的内径不计，当小球运动到轨道最高点时，圆轨道对地面的压力刚好为零，则下列判断正确的是（　　）
A．小球运动的最小速度为$\sqrt{gR}$
B．圆轨道对地面的最大压力为10mg
C．当小球离挡板N最近时，圆轨道对挡板N的压力大小为5mg
D．圆轨道对挡板M、N的压力总是为零
17．如图所示，N为金属板，M为金属网，它们分别与电池的两极相连，各电池的电动势和极性如图所示，己知金属板的逸出功为4.8eV．现分别用不同频率的光照射金属板（各光子的能量已在图上标出），则下列说法正确的是（　　）
A．A图中无光电子射出
B．B图中光电子到达金属板时的动能大小为1.5eV
C．C图中的光电子能到达金属网
D．D图中光电子到达金属板时的最大动能为3.5eV
18．如图所示，在光滑水平面上有ABC三个质量均为m的小球，A带正电，B带负电，C不带电，A，B带电量的绝对值均为Q，B，C两个小球用绝缘细绳连接在一起，当用外力F拉着A球向右运动时，B，C也跟着A球一起向右运动，在运动过程中三个小球保持相对静止共同运动，则（　　）
A．BC间绳的拉力大小为$\frac{2}{3}$FB．BC间绳的拉力大小为$\frac{1}{3}$F
C．AB两球间距为$\sqrt{\frac{3K{Q}^{2}}{2F}}$D．AB两球间距为$\sqrt{\frac{3K{Q}^{2}}{F}}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网