题目内容
 如图所示,直角三角形ABC中存在一匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,
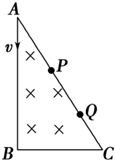
如图所示,直角三角形ABC中存在一匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,分别从AC边上的P、Q两点射出,则( )
分析:粒子在磁场中做圆周运动,根据题设条件作出粒子在磁场中运动的轨迹,根据轨迹分析粒子运动半径和周期的关系,从而分析得出结论.
解答: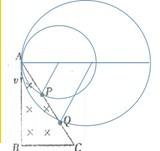 解:粒子在磁场中做匀速圆周运动,根据几何关系(图示弦切角相等),粒子在磁场中偏转的圆心角相等,根据粒子在磁场中运动的时间:
解:粒子在磁场中做匀速圆周运动,根据几何关系(图示弦切角相等),粒子在磁场中偏转的圆心角相等,根据粒子在磁场中运动的时间:
t=
T,又因为粒子在磁场中圆周运动的周期T=
,可知粒子在磁场中运动的时间相等,故D正确,C错误;
如图,粒子在磁场中做圆周运动,分别从P点和Q点射出,由图知,粒子运动的半径RP<RQ,又粒子在磁场中做圆周运动的半径R=
知粒子运动速度vP<vQ,故A错误,B正确;
故选BD
 解:粒子在磁场中做匀速圆周运动,根据几何关系(图示弦切角相等),粒子在磁场中偏转的圆心角相等,根据粒子在磁场中运动的时间:
解:粒子在磁场中做匀速圆周运动,根据几何关系(图示弦切角相等),粒子在磁场中偏转的圆心角相等,根据粒子在磁场中运动的时间:t=
| θ |
| 2π |
| 2πm |
| qB |
如图,粒子在磁场中做圆周运动,分别从P点和Q点射出,由图知,粒子运动的半径RP<RQ,又粒子在磁场中做圆周运动的半径R=
| mv |
| Bq |
故选BD
点评:粒子在磁场中做圆周运动,洛伦兹力提供向心力,由此根据运动特征作出粒子在磁场中运动的轨迹,掌握粒子圆周运动的周期、半径的关系是解决本题的关键.

练习册系列答案
相关题目
 如图所示,直角三角形的斜边倾角为30°,底边BC处在水平位置,斜边AC是光滑绝缘,在底边中点O处放置一正电荷Q.一个带负电的质点从斜面顶端A沿斜边滑下,在质点从斜面滑至C点的运动中( )
如图所示,直角三角形的斜边倾角为30°,底边BC处在水平位置,斜边AC是光滑绝缘,在底边中点O处放置一正电荷Q.一个带负电的质点从斜面顶端A沿斜边滑下,在质点从斜面滑至C点的运动中( ) 如图所示,直角三角形线框abc固定在匀强磁场中,ab是一段长为L电阻为R的均匀导线,ac和bc的电阻可不计,ac长度为
如图所示,直角三角形线框abc固定在匀强磁场中,ab是一段长为L电阻为R的均匀导线,ac和bc的电阻可不计,ac长度为 如图所示,直角三角形支架ABC的边长AB=20cm,BC=15cm,AB边水平.在A点通过细绳挂着一个重30N的物体,求AB和AC杆受到的作用力的大小和方向.
如图所示,直角三角形支架ABC的边长AB=20cm,BC=15cm,AB边水平.在A点通过细绳挂着一个重30N的物体,求AB和AC杆受到的作用力的大小和方向. 如图所示,直角三角形的斜边倾角为30°.底边BC长为2L,处在水平位置,斜边AC是光滑绝缘的.在底边中点O点处放置一正电荷Q,一个质量为m,电荷量为q的带负电的质点从斜面顶端沿斜边滑下,滑到斜边上的垂足D时速度为v.试求
如图所示,直角三角形的斜边倾角为30°.底边BC长为2L,处在水平位置,斜边AC是光滑绝缘的.在底边中点O点处放置一正电荷Q,一个质量为m,电荷量为q的带负电的质点从斜面顶端沿斜边滑下,滑到斜边上的垂足D时速度为v.试求 如图所示,直角三角形OAC(a=300)区域内有B=0.5T的匀强磁场,方向如图所示.两平行极板M、N接在电压为u的直流电源上,左板为高电势.一带正电的粒子从靠近M板由静止开始加速,从N板的小孔射出电场后,垂直OA的方向从P点进入磁场中.带电粒子的比荷为
如图所示,直角三角形OAC(a=300)区域内有B=0.5T的匀强磁场,方向如图所示.两平行极板M、N接在电压为u的直流电源上,左板为高电势.一带正电的粒子从靠近M板由静止开始加速,从N板的小孔射出电场后,垂直OA的方向从P点进入磁场中.带电粒子的比荷为