题目内容
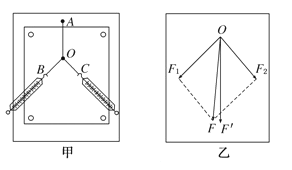
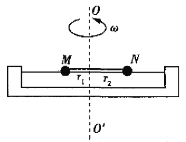
【题目】如图所示为一水平的转台,转台上固定一长直杆,质量分别为
、
的可视为质点的小球M、N穿过长直杆并用质量不计的轻绳
始终处于伸直状态
拴接,环绕
轴转动,当稳定时小球M、N距离转轴的距离分别为
、
,已知
、
,两球与长直杆之间的动摩擦因数均为
,且最大静摩擦力等于滑动摩擦力。当转台的角速度大小为
时拴接两球的轻绳刚好产生作用力,当转台的角速度大小为
时,其中的一个小球所受的摩擦力刚好为零。
（1）轻绳刚好产生作用力时的角速度应为多大？此时两球所受的摩擦力分别为多大？
（2）其中的一个小球所受的摩擦力刚好为零时的角速度应为多大？此时拴接两球的轻绳的作用力应为多大？
【答案】（1）
， 
，
；（2）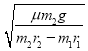
，
【解析】
（1）对小球受力分析，开始加速度较小时，静摩擦力提供小球转动的向心力，有：
；
当其中一个小球所受的静摩擦力达到最大
时，轻绳才提供拉力；
则有：
，
解得：
；
由于
，所以当N受到的摩擦力最大时，轻绳开始产生拉力，此时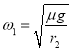
；
此时两小球受到的摩擦力分别为：
，
；
即：轻绳刚好产生作用力时的角速度
应为
，此时两球所受的摩擦力分别为、；
（2）当角速度
时，设轻绳的拉力大小为F：
对小球M，有：
对小球N，有：
；
联立解得小球M受到的摩擦力：
；
由于
、，则小球M受到的静摩擦力随角速度的增大而减小，当减小为0时，转台的角速度为：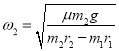
；
由以上可解得此时轻绳的作用力
；
即：其中的一个小球所受的摩擦力刚好为零时的角速度
应为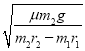
，此时拴接两球的轻绳的作用力应为
。
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
