��Ŀ����
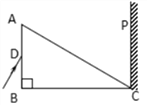
����Ŀ����ͼ��ʾ���ռ����ƽ�С����Ϳ���Ҳ��ΪL��I��II������I��II�������д�ֱ��ֽ�����ǿ�ų���I����ų����ڡ��Ÿ�Ӧǿ��ΪB0��II����ų����⣬��С����������һ����Ϊm�������Ϊ-q�Ĵ������ӣ���ͼ����ʾ��һ���ٵ糡�е�MN�帽���ɾ�ֹ�ͷű����٣����Ӿ��糡���ٺ�ƽ��ֽ����I���ų��߽��45���ǽ���ų���Ȼ���ִ�I���ұ߽��45���������

(1)����ٵ糡���������Ʋ�U���Լ�������I���˶�ʱ��t1��
(2)��II���Ÿ�Ӧǿ��Ҳ��B0ʱ�������Ӿ���I������ߵ�;���II������͵�֮��ĸ߶Ȳ��Ƕ��١�
(3)Ϊʹ�����ܷ���I����II���ĴŸ�Ӧǿ��BӦ����ʲô���������Ӵ�������I������������I����Ҫ���ʱ�䡣
���𰸡���1��![]()
![]() ��2��
��2��![]() ��3��
��3��![]() ��
�� ![]() ��
��
����������1�����������ڴų����˶���ʾ��ͼ����ͼ��ʾ��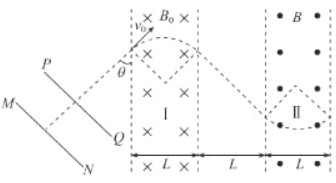
�����ڼ��ٵ糡�и��ݶ��ܶ����ɵã�qU=![]() mv2
mv2
������I������Բ���˶����������������ṩ�������ɵã�qvB0=m![]()
���ݼ��ι�ϵ�ɵã�R1=![]() L
L
�����ɵü��ٵ糡���������Ʋ![]()
�����ڴų����˶������ڣ�![]()
�����ڴų���ת����Բ�Ľ�Ϊ90�����ɵ�������I�����˶���ʱ�䣺![]()
��2��������II�����˶��İ뾶��I������ͬ���߶Ȳ���ͼ�м��ι�ϵ�ɵã�h=��R1+R2����1-cos�ȣ�+Ltan��
�ɵã�h=![]() L
L
��3���������Ӹպô�II�����ұ߽紩���ų����ٽ�״̬�����켣Բ���ұ߽����е������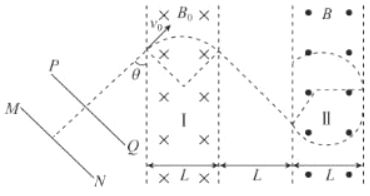
���ݼ��ι�ϵ�ɵã�R2��1+cos�ȣ���L������![]()
��ã�B��![]() B0
B0
��֪��B=![]() B0ʱ��������II�������˶���ʱ������������Ӵ��������������������������ʱ���������������I�����˶���ʱ��Ϊ��t1=2
B0ʱ��������II�������˶���ʱ������������Ӵ��������������������������ʱ���������������I�����˶���ʱ��Ϊ��t1=2![]()
![]()
���������ڴų�֮���ʱ��Ϊ��![]()
������II�����˶���ʱ�䣺![]()
��ʱ�䣺t=t1+t2+t3=��3![]() ��-2��+4��
��-2��+4��![]()