题目内容
【题目】如图所示,水平传送带逆时针匀速转动,速度大小为8m/s,A、B为两轮圆心正上方的点,
AB=L1=6 m,两边水平面分别与传送带表面无缝对接,弹簧右端固定,自然长度时左端恰好位于B点,现将一小物块与弹簧接触(不栓接),并压缩至图示位置然后释放,已知小物块与各接触面间的动摩擦因数均为μ=0.2,AP=L2=5m,小物块与轨道左端P碰撞无机械能损失,小物块最后刚好能返回到B点减速到零,g=10m/s2,则下列说法正确的是( )
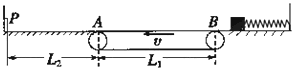
A. 小物块从释放后第一次到B点的过程中,做加速度减小的加速运动
B. 小物块第一次从B点到A点的过程中,一定做匀加速直线运动
C. 小物块第一次到A点时,速度大小一定等于8m/s
D. 小物块离开弹簧时的速度一定满足
【答案】CD
【解析】
由动能定理求出物体返回B点时速度为零的条件，然后分析物体以不同速度滑上传送带后的运动情况，看各选项的速度是否符合要求。
小物块从释放后第一次到B点的过程中，先做加速度减小的加速运动，当弹力小于摩擦力时做加速度增大的减速运动，故A错误；设物体到达P点的速度为v，反弹后运动到B点的速度为零，由动能定理得：
，解得
，物体由A到P点过程中，由动能定理得：
，解得
，小物块第一次从B点到A点的过程中，先做匀减速直线运动，故B错误，C正确；若物体速度较大，一直做匀减速运动，有：
，解得
，若速度较小，在AB上一直加速，到A点时恰好与带同速，有：
，
，联立解得
，故小物块离开弹簧时的速度一定满足
，故D正确；故选CD。
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
