题目内容
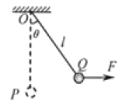
【题目】如图所示，平面直角坐标系xoy在竖直平面内，第三象限内有水平向左的匀强电场，第四象限内y轴与x=2R虚线之间有竖直向下的匀强电场，两电场的电场强度大小均为E，x=3R处有一竖直固定的光屏。现在第三象限内固定一个半径为R的四分之一光滑圆弧轨道AB，圆弧圆心在坐标原点O，A端点在x轴上，B端点在y轴上。一个带电小球从A点上方高2R处的P点由静止释放，小球从A点进入圆弧轨道运动，从B点离开时速度的大小为2
，重力加速度为g，求：
(1)小球的电荷量及其电性；
(2)小球最终打在荧光屏上的位置距x轴的距离。
【答案】（1）小球带正电且带电量大小为
；（2）3.125R
【解析】
（1）设小球带正电且带电量大小为q，小球从P点运动到B点的过程，根据动能定理有
解得
则假设成立，即小球带正电，且带电量大小为。
（2）由于电场力方向向下，且有
qE=mg
小球从B点以
的速度进入第四象限内的电场做类平抛运动，加速度
在电场中运动的时间
下落的高度
出电场时竖直方向的分速度
出电场后至打在光屏上运动的时间
出电场后至打到光屏上在竖直方向运动的距离
因此小球打在荧光屏上的位置距x轴的距离
练习册系列答案
特高级教师点拨系列答案
相关题目
