题目内容
8. 如图所示是位于X星球表面附近的竖直光滑圆弧轨道,宇航员通过实验发现,当小球位于轨道最低点的速度不小于v0时,就能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,X星球的半径为R,万有引力常量为G.则( )
如图所示是位于X星球表面附近的竖直光滑圆弧轨道,宇航员通过实验发现,当小球位于轨道最低点的速度不小于v0时,就能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,X星球的半径为R,万有引力常量为G.则( )| A. | 环绕X星球的轨道半径为2R的卫星的周期为$\frac{4π}{{v}_{0}}$$\sqrt{Rr}$ | |
| B. | X星球的平均密度为$\frac{3{{v}_{0}}^{2}}{10πGRr}$ | |
| C. | X星球的第一宇宙速度为v0$\sqrt{\frac{R}{r}}$ | |
| D. | X星球的第一宇宙速度为v0$\sqrt{\frac{R}{5r}}$ |
分析 小球刚好能在竖直面内做完整的圆周运动,有重力充当向心力,小球在光滑圆弧轨道运动的过程中,根据动能定理得出重力加速度的大小,根据万有引力提供向心力,以及万有引力等于重力,联立解出环月卫星的周期,根据万有引力等于重力求出X星球质量,从而求出密度,根据万有引力提供向心力,以及万有引力等于重力,求第一宇宙速度.
解答 解:A、设X星球表面重力加速度为g,质量为M,小球刚好能做完整的圆周运动;则小球在最高点时,仅由重力提供向心力;根据牛顿第二定律有:
mg=$m\frac{{v}^{2}}{r}$
小球从轨道最高点到最低点的过程中,由动能定理有:
mg•2r=$\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}m{v}^{2}$
联立两式可得:g=$\frac{{{v}_{0}}^{2}}{5r}$
环绕X星球的轨道半径为2R的卫星由万有引力提供向心力,有
$G\frac{Mm}{(2R)^{2}}=m\frac{4{π}^{2}•2R}{{T}^{2}}$
又$G\frac{Mm}{{R}^{2}}=mg$
解得:T=$\frac{4π}{{v}_{0}}\sqrt{10Rr}$,故A错误;
B、根据$G\frac{Mm}{{R}^{2}}=mg$得:
M=$\frac{g{R}^{2}}{G}$
根据M=$ρ•\frac{4}{3}π{R}^{3}$得:$ρ=\frac{M}{V}=\frac{3{{v}_{0}}^{2}}{20πGRr}$,故B错误;
C、X星球的第一宇宙速度为
v=$\sqrt{gR}$=v0$\sqrt{\frac{R}{5r}}$,故C错误,D正确.
故选:D
点评 解决本题的关键会运用机械能守恒定律定律解题,知道小球在内轨道运动恰好过最高点的临界条件.以及掌握万有引力提供向心力和万有引力等于重力.

 阅读快车系列答案
阅读快车系列答案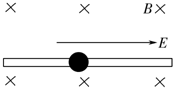 如图所示,在纸面内水平向右的水平匀强电场和垂直纸面向里的水平匀强磁场中,有一水平的固定绝缘杆,小球P套在杆上,小球P套在杆上,P的质量为m,电量为-q,P与杆间的动摩擦因数为μ,电场强度为E,磁感应强度为B,重力沿纸面向下,小球由静止起开始滑动,设电场、磁场区域足够大,杆足够长.在运动过程中小球最大加速度为a0,最大速度为v0,则下列判断正确的是( )
如图所示,在纸面内水平向右的水平匀强电场和垂直纸面向里的水平匀强磁场中,有一水平的固定绝缘杆,小球P套在杆上,小球P套在杆上,P的质量为m,电量为-q,P与杆间的动摩擦因数为μ,电场强度为E,磁感应强度为B,重力沿纸面向下,小球由静止起开始滑动,设电场、磁场区域足够大,杆足够长.在运动过程中小球最大加速度为a0,最大速度为v0,则下列判断正确的是( )| A. | 当a=$\frac{1}{2}$a0时小球的加速度一定增大 | |
| B. | 当v=$\frac{1}{2}$v0时小球的加速度一定减小 | |
| C. | 当a=$\frac{1}{2}$a0时小球的速度v与v0之比$\frac{v}{{v}_{0}}$一定大于$\frac{1}{2}$ | |
| D. | 当v=$\frac{1}{2}$v0时小球的加速度a与a0之比$\frac{a}{{a}_{0}}$一定大于$\frac{1}{2}$ |
| A. | 要研究地球自转时候的轨迹,因为地球相对于太阳来说形状、大小都可以忽略,所以此时的地球可以看做质点 | |
| B. | 小明参加100m跑,前50m的平均速度为7m/s,后50m的平均速度为4m/s,总共花了20s,则全程的平均速度为5m/s. | |
| C. | 永州四中2015年的运动会于11月25号8点正式开幕,这里的8点指的是时间 | |
| D. | 郴州一中2015年的运动会中,若研究长跑运动员的摆臂姿势,则长跑的运动员可以看做质点 |

| A. | 在两板间插入电介质 | B. | 在两板间插入一块厚铝板 | ||
| C. | 将极板B向右适当移动 | D. | 将极板B向上适当移动 |
| A. | 12:22:32 | B. | 1:3:5 | C. | 1:2:3 | D. | 不能确定 |
| A. | 小船渡河的位移一定大于50m | |
| B. | 小船渡河的速度一定小于等于5m/s | |
| C. | 小船渡河的最短时间为12.5s | |
| D. | 若船头指向不变,则小船渡河时将作匀速直线运动 |
 如图所示,水平面上有电阻不计的U形导轨MN、PQ,它们之间的宽度为L=0.2m.M和P之间接入电动势为E=4V、内阻为r=1Ω的电源.现垂直于导轨放置一根质量为m=0.2kg的金属棒.金属棒ab接入导轨间的电阻为R=1Ω,并加一个范围较大的匀强磁场,磁感应强度大小为B=5T,方向竖直向上.金属棒与导轨间的动摩擦因数为μ=0.75.(g=10m/s2)
如图所示,水平面上有电阻不计的U形导轨MN、PQ,它们之间的宽度为L=0.2m.M和P之间接入电动势为E=4V、内阻为r=1Ω的电源.现垂直于导轨放置一根质量为m=0.2kg的金属棒.金属棒ab接入导轨间的电阻为R=1Ω,并加一个范围较大的匀强磁场,磁感应强度大小为B=5T,方向竖直向上.金属棒与导轨间的动摩擦因数为μ=0.75.(g=10m/s2) 某学习小组利用单摆,采用如图所示的实验装置测量重力加速度.
某学习小组利用单摆,采用如图所示的实验装置测量重力加速度. 如图所示,光滑的半圆槽内,A球从高h处沿槽自由滑下,与静止在槽底的B球相碰,若碰撞后A球和B球到达的最大高度均为$\frac{h}{9}$,A球、B球的质量之比为1:4或1:2.
如图所示,光滑的半圆槽内,A球从高h处沿槽自由滑下,与静止在槽底的B球相碰,若碰撞后A球和B球到达的最大高度均为$\frac{h}{9}$,A球、B球的质量之比为1:4或1:2.