题目内容
 如图在光滑的水平杆上穿两个重均为2N的球A、B,在两球之间夹一弹簧,弹簧的劲度系数为10N/m,用两条等长的线将球C与A、B相连,此时弹簧被压短l0cm,两条线的夹角为600,求:
如图在光滑的水平杆上穿两个重均为2N的球A、B,在两球之间夹一弹簧,弹簧的劲度系数为10N/m,用两条等长的线将球C与A、B相连,此时弹簧被压短l0cm,两条线的夹角为600,求:(1)C球重力多大?
(2)杆对A球支持力多大?
分析:根据胡克定律求出弹簧的弹力大小.对A或B研究,由平衡条件求出细线的拉力大小,再对C球研究,由平衡条件求解C球的重力.
解答:解:根据胡克定律得,弹簧的弹力大小为F=kx=10×0.1=1N.
分析A球的受力情况,如图所示,根据平衡条件得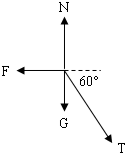
Tcos60°=F
N=G+Tsin60°
解得,T=2N,N=(2+
)N,即杆对A球支持力为(2+
)N
对C球:2Tsin60°=GC,解得,C球重力GC=2
N.
答:(1)C球重力为2
N.
(2)杆对A球支持力2+
N.
分析A球的受力情况,如图所示,根据平衡条件得

Tcos60°=F
N=G+Tsin60°
解得,T=2N,N=(2+
| 3 |
| 3 |
对C球:2Tsin60°=GC,解得,C球重力GC=2
| 3 |
答:(1)C球重力为2
| 3 |
(2)杆对A球支持力2+
| 3 |
点评:本题采用隔离法研究多个物体平衡的问题,分析受力情况,作出力图是解答的基础.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图所示,质量分别为m1、m2的小球A、B可以在光滑的水平杆上滑动,两球之间用一根水平细线相连,m1=2m2.当装置以角速度ω绕中心轴线匀速转动,达到稳定时,两球离轴的距离保持不变,则有( )
如图所示,质量分别为m1、m2的小球A、B可以在光滑的水平杆上滑动,两球之间用一根水平细线相连,m1=2m2.当装置以角速度ω绕中心轴线匀速转动,达到稳定时,两球离轴的距离保持不变,则有( ) (2013?东至县一模)如图所示,在光滑的水平杆上,穿两个重力均为2N的球A、B.在两球之间夹一弹簧,弹簧的劲度系数为10N/m.用两条等长的线将球C与A、B相连,此时弹簧被压缩了10cm两条线的夹角为60°,下列说法正确的是( )
(2013?东至县一模)如图所示,在光滑的水平杆上,穿两个重力均为2N的球A、B.在两球之间夹一弹簧,弹簧的劲度系数为10N/m.用两条等长的线将球C与A、B相连,此时弹簧被压缩了10cm两条线的夹角为60°,下列说法正确的是( )
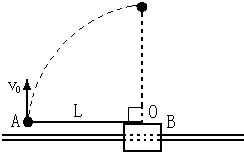 (2006?盐城模拟)如图所示,质量为M的滑块B套在光滑的水平杆上可自由滑动,质量为m的小球A用一长为L的轻杆与B上的O点相连接,轻杆处于水平位置,可绕O点在竖直面内自由转动.
(2006?盐城模拟)如图所示,质量为M的滑块B套在光滑的水平杆上可自由滑动,质量为m的小球A用一长为L的轻杆与B上的O点相连接,轻杆处于水平位置,可绕O点在竖直面内自由转动.