题目内容
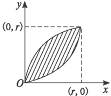
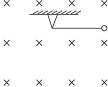
如图11-3-13所示,在xOy平面内,有许多电子(质量为m、电荷量为e)从坐标原点O不断地以速率v0沿不同方向射入第一象限,现加上一个垂直xOy平面的方向垂直纸板面向里的匀强磁场,磁感应强度为B.要求这些电子穿过磁场后都能平行于x轴正方向运动,试求符合该条件的磁场的最小面积.
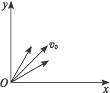
图11-3-13

图11-3-13
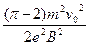
速度大小相同、方向不同的电子在磁场中做圆周运动的半径r一定,即r=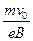 . ①
. ①
如图所示,设任一电子速度v0与x轴夹角为θ,经磁场偏转到速度方向变为平行x轴向右时的位置为P,P点坐标为(x,y),则有:
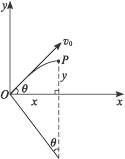
x=r·sinθ ②
y=r-rcosθ ③
由②③式消去θ可得:
x2+(y-r)2=r2
由上式可以看出P点位置在一个圆心为(0,r)、半径为r的圆上的一段弧,此段圆弧应作为磁场的一个边界.
又沿+y方向射入的电子的偏转轨迹是在以r为半径、以(r,0)为圆心的圆上,要使磁场面积为最小面积,由几何知识得:
Smin=2(S扇-S△)=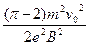 .
.
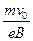 . ①
. ①如图所示,设任一电子速度v0与x轴夹角为θ,经磁场偏转到速度方向变为平行x轴向右时的位置为P,P点坐标为(x,y),则有:

x=r·sinθ ②
y=r-rcosθ ③
由②③式消去θ可得:
x2+(y-r)2=r2
由上式可以看出P点位置在一个圆心为(0,r)、半径为r的圆上的一段弧,此段圆弧应作为磁场的一个边界.
又沿+y方向射入的电子的偏转轨迹是在以r为半径、以(r,0)为圆心的圆上,要使磁场面积为最小面积,由几何知识得:

Smin=2(S扇-S△)=
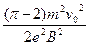 .
.
练习册系列答案
相关题目
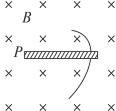

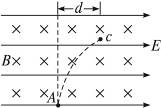
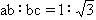 的长方形区域abcd内,有垂直纸面向里的匀强磁场,一束速率不同的电子,从b点沿平行边界bc方向射入磁场中,从a点和d点有电子射出磁场,则从a点和d点射出的电子的速率之比为[ ]
的长方形区域abcd内,有垂直纸面向里的匀强磁场,一束速率不同的电子,从b点沿平行边界bc方向射入磁场中,从a点和d点有电子射出磁场,则从a点和d点射出的电子的速率之比为[ ]
