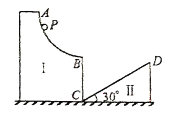
题目内容
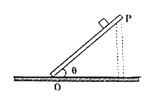
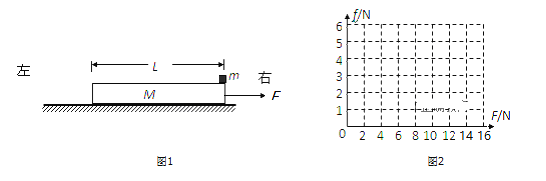
【题目】如图所示,一段不可伸长的轻质细绳长为L,一端固定在O点,另一端系一个质量为m的小球(可以视为质点),保持细绳处于伸直状态,把小球拉到跟O点等高的位置由静止释放,在小球摆到最低点的过程中,不计空气阻力,重力加速度大小为g,则( )
A. 合力做的功为0 B. 合力做的冲量不为0
C. 重力做的功为mgL D. 重力的冲量为m![]()
【答案】BC
【解析】
根据机械能守恒即可求出小球在最低点的速度,根据动量定理即可求出合力的冲量,由动能定理求出重力做的功;
A、小球在向下运动的过程中,受到重力和绳子的拉力,绳子的拉力始终与运动的方向垂直,所以只有重力做功,合外力做的功等于重力做的功,大小为![]() ,故A错误,C正确;
,故A错误,C正确;
B、由机械能守恒可得,小球在最低点的动能:![]()
所以速度:![]()
由动量定理可得合力的冲量大小为:![]() ,不为零,可知重力的冲量不等于
,不为零,可知重力的冲量不等于![]() ,故B正确,D错误。
,故B正确,D错误。

【题目】某课题小组通过实验测量河水的电阻率.现备有一根均匀的长玻璃管(两端各有一个可移动圆形电极,可装入样品水,接触电阻不计)、直尺、待测的水样品.电路器材如表一,他们用伏安法多次测量的数据如表二(为实验处理的方便,实验时每次都把电流表示数调到相同);实验中还用10分度的游标卡尺测量了玻璃管的内径,结果如图甲所示.
表一
器材编号 | 器材名称 | 规格 |
1 | 电流表 | 200 μA,内阻约10 Ω |
2 | 电压表 | 12 V,内阻约100 kΩ |
3 | 电池组 | 12 V,内阻不计 |
4 | 滑动变阻器 | 10 Ω 1 A |
5 | 开关 | |
6 | 导线 | 若干 |
7 | 定值电阻 | 100 Ω |
表二
序号 | 水柱长度/cm | 电压表示数/V | 电流表示数/μA |
1 | 10 | 2 | 100 |
2 | 20 | 4 | 100 |
3 | 30 | 6 | 100 |
4 | 40 | 8 | 100 |
5 | 50 | 10 | 100 |
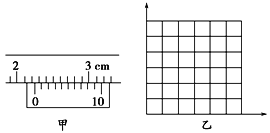
(1)玻离管内径d的测量值为________ cm.
(2)根据表一器材和表二数据确定测量电路中电流表应该________(填“内接”或“外接”),电路的连接方式应该采用________(填“分压电路”或“限流电路”).
(3)用计算出的水柱长度L与水柱电阻R在图乙中描点,画出R-L图象______(要求标出坐标轴的物理量、单位和对应的数值).
(4)计算出所测水的电阻率为________ Ω·m.