题目内容
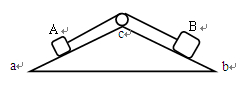
如图所示，物体的重量为2kg，两根轻绳AB和AC的一端连接于竖直墙上，另一端系于物体上，在物体上另施加一个方向与水平线成θ=60°的拉力F，若要使两绳都能伸直，求拉力F的大小范围。
解析试题分析：作出物体A受力如图所示，由平衡条件
Fy=Fsinθ+F1sinθ-mg=0 ①
Fx=Fcosθ-F2-F1cosθ=0 ②
由①②式分别得：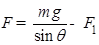
③
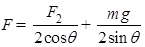④
要使两绳都能绷直，则有：F1≥0 ⑤；F2≥0 ⑥
由③⑤式得F有最大值：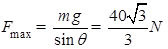
．
由④⑥式得F有最小值：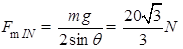
综合得F的取值范围：．
考点：物体的平衡；正交分解法。
练习册系列答案
阅读快车系列答案
相关题目
如图所示，将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器底部
处（O为球心），弹簧另一端与质量为m的小球相连，小球静止于P点。已知容器半径为R，与水平面间的动摩擦因数为
，OP与水平方向的夹角为
。下列说法正确的是（ ）
| A．容器相对于水平面有向左运动的趋势 |
B．轻弹簧对小球的作用力大小为 |
| C．容器对小球的作用力竖直向上 |
D．弹簧原长为 |
为30°的斜面向上。绝缘斜面上固定有
形状的光滑金属导轨MPN（电阻忽略不计），MP和NP长度均为2.5m，MN连线水平，长为3m。以MN中点O为原点、OP为x轴建立一维坐标系Ox。一根粗细均匀的金属杆CD，长度d为3m、质量m为1kg、电阻R为0.3Ω，在拉力F的作用下，从MN处以恒定的速度v=1m/s，在导轨上沿x轴正向运动（金属杆与导轨接触良好）。g取10m/s2。
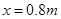处电势差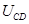
；
、并垂直于ab的匀强磁场；倾斜导轨间有沿斜面向下的匀强磁场，磁感应强度均为B。倾斜导轨与水平面夹角也为
. ab杆在水平恒力作用下由静止开始运动，当cd刚要滑动时ab恰达到最大速度 . （
、
、最大静摩擦力等于滑动摩擦力）.求：
，则cd产生的焦耳热Q为多大？