题目内容
如图所示,在水平桌面上固定着一个水平放置的光滑圆轨道,在轨道的B点静止着一个质量为m2的弹性小球乙,另一个质量为m1的弹性小球甲以初速度Vo运动,与乙球发生第一次碰撞后,恰在C点发生第二次碰撞。若碰撞过程中没有动能损失,则甲、乙两球的质量之比m1: m2可能等于


| A. 5:3 | B. 9:1 | C.1:7 | D.3:5 |
ACD
解答:解:设碰撞后m1、m2的速度分别为v1、v2.由题分析得到,m1碰后必然反向.
第一种情况:m1小球由A到B撞m2过程:以v0方向为正,由动量守恒定律得:m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,在相同时间内,线速度大小与路程成正比,则有:3v2=v1…②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得: m1v02=
m1v02= m1v12+
m1v12+ m2v22…③
m2v22…③
将②代人①③得:m1(v0+3v2)=m2v2
m1(v02-9v22)=m2v22
两式相除得v0=4v2
再代入①解得m1:m2=1:7
第二种情况:m1小球由A到D到C再到B撞m2过程:以v0方向为正,
由动量守恒定律得:m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,故有:v2=3v1…②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得: m1v02=
m1v02= m1v12+
m1v12+ m2v22…③
m2v22…③
解得:m1:m2=3:5
故选CD
点评:本题碰撞前小球m1的运动方向可能存在两种情况,碰撞遵守动量守恒和机械能守恒.关键是根据圆周运动知识的规律研究碰撞后速度的关系.
第一种情况:m1小球由A到B撞m2过程:以v0方向为正,由动量守恒定律得:m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,在相同时间内,线速度大小与路程成正比,则有:3v2=v1…②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得:
 m1v02=
m1v02= m1v12+
m1v12+ m2v22…③
m2v22…③将②代人①③得:m1(v0+3v2)=m2v2
m1(v02-9v22)=m2v22
两式相除得v0=4v2
再代入①解得m1:m2=1:7
第二种情况:m1小球由A到D到C再到B撞m2过程:以v0方向为正,
由动量守恒定律得:m1v0=m2v2-m1v1…①
因为恰在C点发生第二次碰撞,故有:v2=3v1…②
且m1、m2为弹性球发生弹性碰撞,由机械能守恒得:
 m1v02=
m1v02= m1v12+
m1v12+ m2v22…③
m2v22…③解得:m1:m2=3:5
故选CD
点评:本题碰撞前小球m1的运动方向可能存在两种情况,碰撞遵守动量守恒和机械能守恒.关键是根据圆周运动知识的规律研究碰撞后速度的关系.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
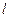 .开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘住物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球到达最高点.求
.开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘住物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球到达最高点.求
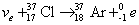 ,其中
,其中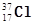 核的质量为36.95658 u;
核的质量为36.95658 u;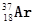 核的质量为36.95691u,
核的质量为36.95691u,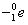 的质量为0.00055u,1u质量对应的能量为931.5MeV根据以上数据,可以判断参与上述核反应的电子中微子的最小能量为 MeV
的质量为0.00055u,1u质量对应的能量为931.5MeV根据以上数据,可以判断参与上述核反应的电子中微子的最小能量为 MeV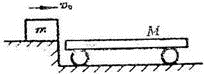
 v0,设木块对子弹的阻力始终保持不变.求:
v0,设木块对子弹的阻力始终保持不变.求:
 =0.2,最大静摩擦力等于滑动摩擦力。小车不带电,g取10 m/s2。求:
=0.2,最大静摩擦力等于滑动摩擦力。小车不带电,g取10 m/s2。求: