题目内容
如图所示,A是置于光滑水平面上的表面绝缘、质量m1="1" kg的小车,小车的左端放置有一个可视为质点的、质量m2=2 kg、电荷量q=+1×10-4 C的小物块B,距小车右端s=2 m处有一竖直的墙壁。小车所在空间有一个可以通过开关控制其有、无的水平向右的匀强电场,电场强度的大小为E=3×104N/C。若小车A和小物块B一起由静止开始运动,且在小车与墙壁碰撞的瞬间撤去电场;碰撞时间忽略不计,碰撞过程无机械能的损失;小物块B始终未到达小车A的右端,它们之问的动摩擦因数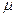 =0.2,最大静摩擦力等于滑动摩擦力。小车不带电,g取10 m/s2。求:
=0.2,最大静摩擦力等于滑动摩擦力。小车不带电,g取10 m/s2。求:
(1)有电场作用时小车A所受的摩擦力大小和方向?
(2)小车A第一次与墙壁相碰后向左运动的最远距离为多少?
(3)小车A第二次与墙壁相碰时的速度为多少?
(4)要使小物块B最终不滑离小车A,小车的长度至少多长?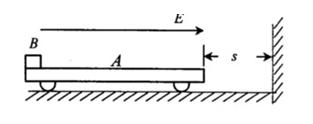
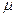 =0.2,最大静摩擦力等于滑动摩擦力。小车不带电,g取10 m/s2。求:
=0.2,最大静摩擦力等于滑动摩擦力。小车不带电,g取10 m/s2。求:(1)有电场作用时小车A所受的摩擦力大小和方向?
(2)小车A第一次与墙壁相碰后向左运动的最远距离为多少?
(3)小车A第二次与墙壁相碰时的速度为多少?
(4)要使小物块B最终不滑离小车A,小车的长度至少多长?

(1)假设小车A与小物块B相对静止,以A、B整体为研究对象
由牛顿第二定律得qE=(m1+m2)a (1分)
解得a=1 m/s2 (1分)
再以小车A为研究对象,设它受到的静摩擦力为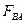 ,A、B之间的最大静摩擦力为
,A、B之间的最大静摩擦力为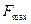 ,
,
由牛顿第二定律得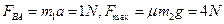 (2分)
(2分)
因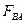 <
<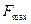 ,故假设成立。小车A所受的摩擦力大小为1N,方向水平向右 (2分)
,故假设成立。小车A所受的摩擦力大小为1N,方向水平向右 (2分)
(2)设小车A和小物块B第一次与墙壁相碰前瞬间的速度为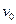 。
。
由运动学规律有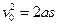 (1分)
(1分)
解得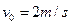 (1分)
(1分)
小车A与墙壁相碰后瞬间速度大小不变,方向向左,小物块B速度不变。由于B的动
量大于A的动量,因此A向左做匀减速运动的速度减为零时,向左运动的距离最远,设这个距离为
由动能定理有 (1分)
(1分)
解得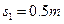 (2分)
(2分)
(3)接着小车A又向右做初速度为零的匀加速运动,假设小车A和小物块B先达到共同速度后再与墙壁相碰,且设第二次与墙壁相碰前瞬间的速度为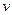 共
共
由动量守恒定律得 (2分)
(2分)
解得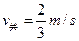 (1分)
(1分)
设小车A由速度为零到达到共同速度所通过的距离为s2
由动能定理有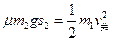 (1分)
(1分)
解得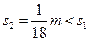 ,所以,假设成立 (1分)
,所以,假设成立 (1分)
 (4)小车A与小物块B最终将停止在墙角处,设小车至少长L
(4)小车A与小物块B最终将停止在墙角处,设小车至少长L
由能量守恒定律得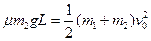 (2分)
(2分)
代入数据得L="1.5" m (2分)
由牛顿第二定律得qE=(m1+m2)a (1分)
解得a=1 m/s2 (1分)
再以小车A为研究对象,设它受到的静摩擦力为
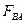 ,A、B之间的最大静摩擦力为
,A、B之间的最大静摩擦力为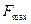 ,
,由牛顿第二定律得
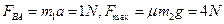 (2分)
(2分)因
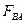 <
<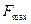 ,故假设成立。小车A所受的摩擦力大小为1N,方向水平向右 (2分)
,故假设成立。小车A所受的摩擦力大小为1N,方向水平向右 (2分)(2)设小车A和小物块B第一次与墙壁相碰前瞬间的速度为
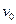 。
。由运动学规律有
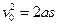 (1分)
(1分)解得
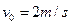 (1分)
(1分)小车A与墙壁相碰后瞬间速度大小不变,方向向左,小物块B速度不变。由于B的动
量大于A的动量,因此A向左做匀减速运动的速度减为零时,向左运动的距离最远,设这个距离为

由动能定理有
 (1分)
(1分)解得
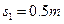 (2分)
(2分)(3)接着小车A又向右做初速度为零的匀加速运动,假设小车A和小物块B先达到共同速度后再与墙壁相碰,且设第二次与墙壁相碰前瞬间的速度为
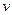 共
共由动量守恒定律得
 (2分)
(2分)解得
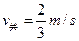 (1分)
(1分)设小车A由速度为零到达到共同速度所通过的距离为s2
由动能定理有
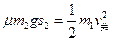 (1分)
(1分)解得
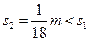 ,所以,假设成立 (1分)
,所以,假设成立 (1分) (4)小车A与小物块B最终将停止在墙角处,设小车至少长L
(4)小车A与小物块B最终将停止在墙角处,设小车至少长L由能量守恒定律得
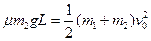 (2分)
(2分)代入数据得L="1.5" m (2分)
略

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目

 ,右侧是光滑的,一轻质弹簧右端固定在墙壁上,左端与静止在O点、质量为 m的小物块A连接,弹簧处于原长状态。 质量为2m的物块B静止在C处, 受到水平瞬时冲量作用后获得向右的速度v0,物块B运动到O点与物块A相碰后一起向右运动,碰撞不粘连(设碰撞时间极短),不计空气阻力。CO=5L,物块B和物块A均可视为质点. 求物块B最终停止的位置离O点多远?
,右侧是光滑的,一轻质弹簧右端固定在墙壁上,左端与静止在O点、质量为 m的小物块A连接,弹簧处于原长状态。 质量为2m的物块B静止在C处, 受到水平瞬时冲量作用后获得向右的速度v0,物块B运动到O点与物块A相碰后一起向右运动,碰撞不粘连(设碰撞时间极短),不计空气阻力。CO=5L,物块B和物块A均可视为质点. 求物块B最终停止的位置离O点多远?
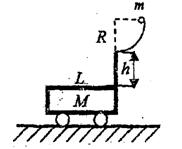
 的小铁块甲相连。开始时,弹簧为原长,甲静止于D点。现将另一与甲完全相同的小铁块乙从圆轨道上B点由静止释放,到达D点与甲碰撞,并立即一起向左运动但不粘连,它们到达E点后再返回,结果乙恰回到C点。已知CD长为L1,DE长为L2,EC段均匀粗糙,ABC段和EF段均光滑,弹簧始终处于弹性限度内。
的小铁块甲相连。开始时,弹簧为原长,甲静止于D点。现将另一与甲完全相同的小铁块乙从圆轨道上B点由静止释放,到达D点与甲碰撞,并立即一起向左运动但不粘连,它们到达E点后再返回,结果乙恰回到C点。已知CD长为L1,DE长为L2,EC段均匀粗糙,ABC段和EF段均光滑,弹簧始终处于弹性限度内。
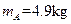 ,长为L=0.50 m,高为h=0.20 m的木块A放在水平地面上,质量为
,长为L=0.50 m,高为h=0.20 m的木块A放在水平地面上,质量为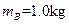 的小木块B(可视为质点)放在木块A的右端,质量为
的小木块B(可视为质点)放在木块A的右端,质量为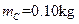 、初速度大小为
、初速度大小为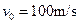 的子弹C从A的左端水平射入并和它一起以共同速度运动(射入时间忽略不计).若A、B之间接触面光滑,A和地面之间的动摩擦因数为
的子弹C从A的左端水平射入并和它一起以共同速度运动(射入时间忽略不计).若A、B之间接触面光滑,A和地面之间的动摩擦因数为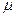 =0.25,取g=10m/
=0.25,取g=10m/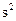 .求:
.求:
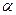 粒子散射实验与枣糕模型和核式结构模型的建立无关
粒子散射实验与枣糕模型和核式结构模型的建立无关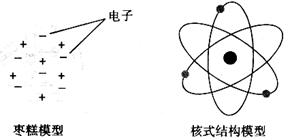
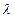 的倒数,这个公式可写作:
的倒数,这个公式可写作: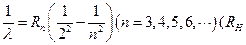 为常数)
为常数)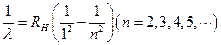 (RH为常数)
(RH为常数)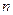 在波尔理论中被称为量子数。玻尔氢原子理论的能级图如图所示。
在波尔理论中被称为量子数。玻尔氢原子理论的能级图如图所示。
 ,该金属的逸出功为______。若用波长为
,该金属的逸出功为______。若用波长为 )单色光做实验,则其遏止电压为______。已知电子的电荷量,真空中的光速和布朗克常量分别为e,c和h。
)单色光做实验,则其遏止电压为______。已知电子的电荷量,真空中的光速和布朗克常量分别为e,c和h。
 沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为
沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为 。求弹簧释放的势能。
。求弹簧释放的势能。