题目内容
【题目】一圆筒的横截面如图所示,圆心为O、半径为R,在筒上有两个小孔M,N且M、O、N在同一水平线上。圆筒所在区域有垂直于圆筒截面的匀强磁场,磁感应强度大小为B,在圆筒左侧有一个加速电场.一个质量为m、电荷量为q的带正电粒子,由静止经电场加速后从M孔沿MO方向射入圆筒.已知粒子与圆筒碰撞时电荷量保持不变,碰撞后速度大小不变,方向与碰撞前相反,不计粒子重力。
(1)若加速电压为U0,要使粒子沿直线MN运动,需在圆筒内部空间加一匀强电场,求所加电场的电场强度大小E;
(2)若带电粒子与圆筒碰撞三次后从小孔N处射出,求粒子在圆筒中运动时间t;

【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】(1)带电粒子在平行板加速过程中,由动能定理得![]()
在磁场中运动时,电场力与洛伦兹力平衡qv0B=qE 解得![]()
(2)带粒子在磁场中运动的周期![]()
带电粒子与环碰撞三次有两种情况:
第一种情况如下图所示,

两次碰撞点与圆环圆心的连线夹角α=![]()
两次碰撞过程粒子通过弧长对应的圆心角β=π–α=![]()
整个过程运动时间![]()
第二种情况如下图所示,
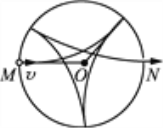
两次碰撞点与圆环圆心的连线夹角α′=![]()
两次碰撞过程粒子通过弧长对应的圆心角β′=π–α′=![]()
整个过程运动时间![]()
所以带电粒子在圆环中运动的时间为![]() 或
或![]()

练习册系列答案
相关题目