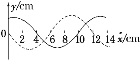��Ŀ����
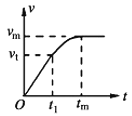
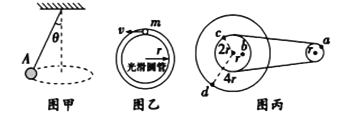
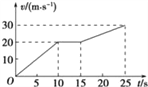
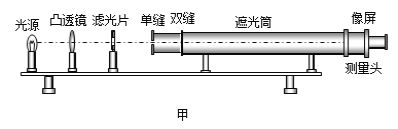
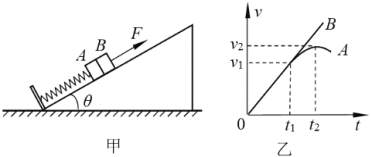
����Ŀ����ͼ����ʾ�����Ϊ���Ĺ⻬б��̶���ˮƽ���ϣ�����ϵ��Ϊk���ᵯ�ɣ��¶˹̶���б��ˣ��϶�������Ϊm�����A���ӣ�A���Ҳ����һ����Ϊm�����B����B��A��ճ������ʼʱ��������ֹ������ƽ����б�����ϵ�����F������B��ʹB�����ٶ�Ϊa���ȼ����˶���������ڿ�ʼһ��ʱ���ڵ�v��tͼ����ͼ����ʾ��t1ʱ��A��B��ͼ�����У�t2ʱ�̶�ӦAͼ�ߵ���ߵ㣬�������ٶ�Ϊg����( )
A. ![]()
B. t2ʱ�̣������α���Ϊ![]()
C. t2ʱ�̵��ɻָ���ԭ�������A�ﵽ�ٶ����ֵ
D. �ӿ�ʼ��t1ʱ�̣�����F���Ĺ��ȵ����ͷŵ�������![]()
���𰸡�BD
��������
��ͼ������t1ʱ��A��B��ʼ���룬��A����ţ�ٵڶ������У�kx-mgsin��=ma����ʼʱ�У�2mgsin��=kx0����x0-x=![]() at12����������ʽ�ã�
at12����������ʽ�ã�![]() ����A������ͼ֪��t2ʱ��A�ļ��ٶ�Ϊ�㣬�ٶ������ţ�ٵڶ����ɺͺ��˶��ɵã�mgsin��=kx����ã�x=
����A������ͼ֪��t2ʱ��A�ļ��ٶ�Ϊ�㣬�ٶ������ţ�ٵڶ����ɺͺ��˶��ɵã�mgsin��=kx����ã�x=![]() ����ʱ���ɴ���ѹ��״̬����B��ȷ��C������ͼ������t1ʱ��A��B��ʼ���룬��A����ţ�ٵڶ����ɣ�kx-mgsin��=ma����
����ʱ���ɴ���ѹ��״̬����B��ȷ��C������ͼ������t1ʱ��A��B��ʼ���룬��A����ţ�ٵڶ����ɣ�kx-mgsin��=ma����
��ʼʱ�У�2mgsin��=kx0����
�ӿ�ʼ��t1ʱ�̣������ͷŵ����� EP=![]() kx02-
kx02- ![]() kx2����
kx2����
�ӿ�ʼ��t1ʱ�̵Ĺ����У����ݶ��ܶ����ã�WF+EP-2mgsin�ȣ�x0-x��= ![]() 2mv12����
2mv12����
2a��x0-x��=v12����
�ɢ٢ڢۢܢݽ�ã�WF-EP=-![]() ����������F���Ĺ��ȵ����ͷŵ�������
����������F���Ĺ��ȵ����ͷŵ�������![]() ����D��ȷ����ѡBD.
����D��ȷ����ѡBD.

 һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�