��Ŀ����
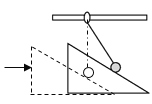
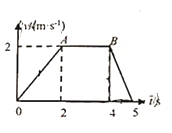
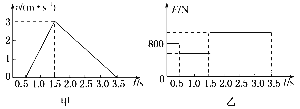
����Ŀ����ͼ��ʾ����������һ�̶���б����ABCD����AB�ߵij���S=2m��б�����Ϊ370��ˮƽ��������һ������M=3Kg���㹻����ľ�������б���徲ֹ���á�����Ϊm=lkg������A�㾲ֹ���£�Ȼ���B�㻬�ϳ�ľ�壨��б�滬����ľ��ʱ�ٶȴ�С���䣩���ڳ�ľ���ϻ���ʱ��Ϊ1.2sʱ�볤ľ����ٶ���ȣ���֪������б����Ķ�Ħ������Ϊ0.25�������볤ľ��Ķ�Ħ������Ϊ0.3��ȡsin370=0.6�� cos370=0.8��g=10m/s2��
��
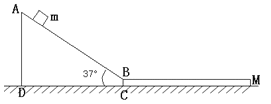
��1�����嵽��б���B��ʱ���ٶȴ�С��
��2����ľ��������Ķ�Ħ��������
��3����ľ�廬�е������롣
���𰸡���1��4m/s��2��0.05��3��0.40
��������
��1������ţ�ٵڶ��������������б���»��ļ��ٶȣ�Ȼ������ٶ�λ�ƹ�ʽ������嵽��б���B��ʱ���ٶȴ�С��
��2�����������ţ�ٵڶ�����������ٶȣ������ٶ������ⳤľ��ļ��ٶȺ�ʱ�䣬�ٸ���ţ�ٵڶ����ɶԳ�ľ���з�����ⳤľ��������Ķ�Ħ������.
��3������λ��ʱ�乫ʽ�����ľ����ٺͼ���ʱ�˶���λ�ƣ��Ӷ����ľ�廬�е������룮
��1����A��B�Ĺ��̣�����ţ�ٵڶ������У�
![]()
��ã�![]()
�»���B��ʱ���ٶȣ�![]()
��ã�![]()
��2�����ϳ�ľ��ʱ�������壬��ţ�ٵڶ����ɵã�![]()
���![]() ����ˮƽ����
����ˮƽ����
�ٶ�����У�![]()
���![]()
�Գ�ľ�壬��ţ�ٵڶ����ɵã�![]()
���![]()
��3����ľ�����λ��Ϊ��![]()
ĩ�ٶ�Ϊ��![]()
����ţ�ٵڶ������У�![]()
![]()
�������![]()
���������![]()